Question

Solve the differential equation by variation of parameters. y'' + y = cos2(x)

Answer 1

`y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-(1)/(3)\sin^4(x)+(1)/(3)\cos^4(x)}}}`

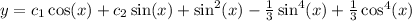
Explanation:

Given the second-order differential equation,
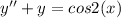`y'' + y = cos2(x)`, solve it using variation of parameters.

(1) - Solve the DE as if it were homogenous and find the homogeneous solution
`y'' + y = cos2(x) \Longrightarrow y'' + y =0\\\\\text{The characteristic equation} \Rightarrow m^2+1=0\\\\m^2+1=0\\\\ \Longrightarrow m^2=-1\\\\\ \Longrightarrow m=√(-1) \\\\\Longrightarrow \boxed{m=\pm i} \\ \\\text{Solution is complex will be in the form} \ \boxed{y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)} \ \text{where} \ m=\alpha \pm \beta i`

`\therefore \text{homogeneous solution} \rightarrow \boxed{y_h=c_1\cos(x)+c_2\sin(x)}`

(2) - Find the Wronskian determinant

`|W|=\left|\begin{array}{ccc}y_1&y_2\\y'_1&y'_2\end{array}\right| \\\\\Longrightarrow |W|=\left|\begin{array}{ccc}\cos(x)&\sin(x)\\-sin(t)&cos(x)\end{array}\right|\\\\\Longrightarrow \cos^2(x)+\sin^2(x)\\\\\Longrightarrow \boxed=1`

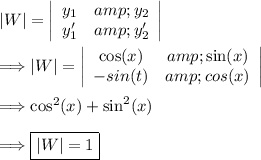
(3) - Find W_1 and W_2

`\boxed{W_1=\left|\begin{array}{ccc}0&y_2\\g(x)&y'_2\end{array}\right| and \ W_2=\left|\begin{array}{ccc}y_2&0\\y'_2&g(x)\end{array}\right|}`

`W_1=\left|\begin{array}{ccc}0&\sin(x)\\\cos^2(x)&\cos(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_1= -\sin(x)\cos^2(x)}\\\\W_2=\left|\begin{array}{ccc}\cos(x)&0\\ -\sin(x)&\cos^2(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_2= \cos^3(x)}`

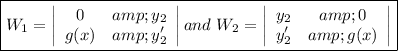
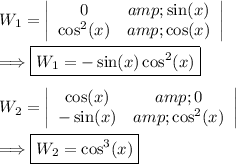
(4) - Find u_1 and u_2

`\boxedW`\

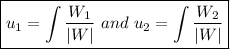u_1:

`\int((-\sin(x)\cos^2(x))/(1)) dx\\\\\Longrightarrow-\int(\sin(x)\cos^2(x)) dx\\\\\text{Let} \ u=\cos(x) \rightarrow du=-sin(x)dx\\\\\Longrightarrow\int u^2 du\\\\\Longrightarrow (1)/(3)u^3\\ \\\Longrightarrow \boxed{u_1=(1)/(3)\cos^3(x)}`

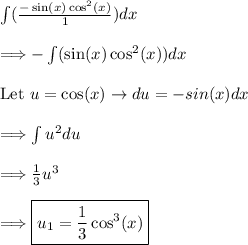
u_2:

`\int(\cos^3(x))/(1)dx\\ \\\Longrightarrow \int \cos^3(x)dx\\\\ \Longrightarrow \int (\cos^2(x)\cos(x))dx \ \ \boxed{\text{Trig identity:} \cos^2(x)=1-\sin^2(x)}\\\\\Longrightarrow \int[(1-\sin^2(x)})\cos(x)]dx\\\\\Longrightarrow \int \cos(x)dx-\int (\sin^2(x)\cos(x))dx\\\\\Longrightarrow \sin(x)-\int (\sin^2(x)\cos(x))dx\\\\\text{Let} \ u=\sin(x) \rightarrow du=cos(x)dx\\\\\Longrightarrow \sin(x)-\int u^2du\\\\\Longrightarrow \sin(x)-(1)/(3) u^3`\

`\Longrightarrow \boxed{u_2=\sin(x)-(1)/(3) \sin^3(x)}`

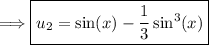
(5) - Generate the particular solution

`\text{Particular solution} \rightarrow y_p=u_1y_1+u_2y_2`

`\Longrightarrow y_p=((1)/(3)\cos(x))(\cos(x))+(\sin(x)-(1)/(3) \sin^3(x))(\sin(x))\\\\ \Longrightarrow y_p=(1)/(3)\cos^4(x)+\sin^2(x)-(1)/(3)\sin^4(x)\\\\\Longrightarrow \boxed{y_p=\sin^2(x)-(1)/(3)\sin^4(x)+(1)/(3)\cos^4(x)}`

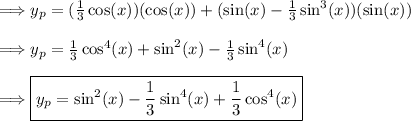
(6) - Form the general solution

`\text{General solution} \rightarrow y_(gen.)=y_h+y_p`

`\boxed{\boxed{y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-(1)/(3)\sin^4(x)+(1)/(3)\cos^4(x)}}}`

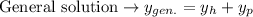
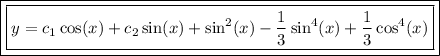
Thus, the solution to the given DE is found where c_1 and c_2 are arbitrary constants that can be solved for given an initial condition. You can simplify the solution more if need be.