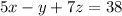Question

Convert this vector equation to cartesian form using the vector product.

r = i - 5j + 4k + λ(3i + j - 2k) + µ(-i + 2j + k)

Answer 1

`5x-y+7z-38=0`

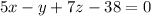
or

`5x-y+7z=38`

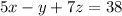
Explanation:

Given vector equation:

`\textbf{r} = \textbf{i} - 5\textbf{j} + 4\textbf{k} + \lambda(3\textbf{i} + \textbf{j} - 2\textbf{k}) + \mu(-\textbf{i} + 2\textbf{j} + \textbf{k})`

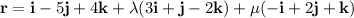
The vector 3i + j - 2k is perpendicular to n.

The vector -i + 2j + k is perpendicular to n.

`\textsf{So}\;\;\textbf{n}=\left|\begin{array}{ccc}\textbf{i}&\textbf{j}&\textbf{k}\\3&1&-2\\-1&2&1\end{array}\right|`

`=\textbf{i}\left|\begin{array}{rr}1&-2\\2&1\end{array}\right|-\textbf{j}\left|\begin{array}{rr}3&-2\\-1&1\end{array}\right|+\textbf{k}\left|\begin{array}{rr}3&1\\-1&2\end{array}\right|`

`=\textbf{i}(1 \cdot 1 - (-2) \cdot 2)-\textbf{j}(3 \cdot 1-(-2) \cdot (-1))+\textbf{k}(3 \cdot 2-1 \cdot (-1))`

`=\textbf{i}(1 +4)-\textbf{j}(3-2)+\textbf{k}(6+1)`

`=5\textbf{i}-\textbf{j}+7\textbf{k}`

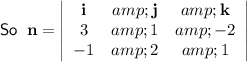
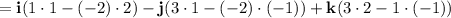
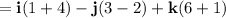
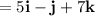
So the equation of the plane written in Cartesian form is:

`5x-y+7z+d=0`

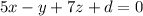
Substituting (1, -5, 4) gives:

`5(1)-(-5)+7(4)+d=0`

`5+5+28+d=0`

`38+d=0`

`d=-38`

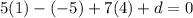
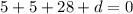
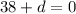
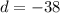
Therefore, the given vector equation in Cartesian form is:

`5x-y+7z-38=0`

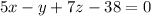
or

`5x-y+7z=38`