Final answer:
The surface area S of the portion of the cone
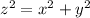 , where
, where
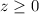 , contained within the cylinder
, contained within the cylinder
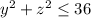 is
is
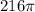 square units.
square units.
Step-by-step explanation:
To find the surface area of the portion S of the cone
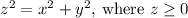 , contained within the cylinder
, contained within the cylinder
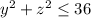 , we'll first parameterize the surfaces of the cone and the cylinder.
, we'll first parameterize the surfaces of the cone and the cylinder.
Given the cone equation
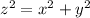 , we can rewrite it in terms of cylindrical coordinates as z = r, where r represents the radial distance from the z-axis.
, we can rewrite it in terms of cylindrical coordinates as z = r, where r represents the radial distance from the z-axis.
In cylindrical coordinates, the equation of the cylinder
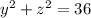 becomes
becomes
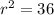 , or simply r = 6.
, or simply r = 6.
The surface area of the portion S of the cone can be obtained by integrating the surface area element over the region described by the cylindrical coordinates.
The surface area element dS for a surface given in cylindrical coordinates is
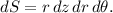
We need to determine the limits of integration for r,
 , and z to cover the region of interest.
, and z to cover the region of interest.
Limits of integration:
- r varies from 0 to 6 (since r = 6 for the cylinder).
-
 will vary from 0 to
will vary from 0 to
 to cover the entire circle around the z-axis.
to cover the entire circle around the z-axis.
- For z, it varies from 0 to the upper boundary defined by the cone equation
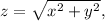 which in cylindrical coordinates is simply
which in cylindrical coordinates is simply
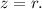
Therefore, the integral for the surface area S of the portion of the cone within the cylinder is:
![\[ S = \int_0^(2\pi) \int_0^6 r \, dz \, dr \, d\theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d0oewi4si40ad9k9aef3zdhbgwxl2jpemm.png)
Solving this integral step by step:
![\[ S = \int_0^(2\pi) \int_0^6 r \, dz \, dr \, d\theta \]\[ = \int_0^(2\pi) \left[ z \right]_0^6 \, dr \, d\theta \]\[ = \int_0^(2\pi) 6r \, dr \, d\theta \]\[ = \left[ 3r^2 \right]_0^6 \, d\theta \]\[ = 3(6)^2 \int_0^(2\pi) d\theta \]\[ = 3(36)(2\pi) \]\[ = 216\pi \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5u8b9hma3k5h8pjwytidbdo731c6jg9brh.png)