Answer: About -4.604.
Explanation:
To solve, we will isolate the x variable.
Given:
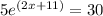
Divide both sides of the equation by 5:

Natural log of both sides:

Power property:
(2x + 11)(Lne) = Ln(6)
Simplify:
➜
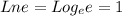
2x + 11 = Ln(6)
Subtract 11 from both sides of the equation:
2x = Ln(6) - 11
Divide both sides of the equation by 2:

Compute:
x = -4.60412 ≈ -4.604