Let
 be one of the numbers. Then the other one is
be one of the numbers. Then the other one is
 .
.
Therefore, the sum of their cubes is:
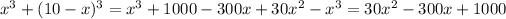
Now we need to find the minimum value of the resulting function.
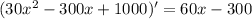
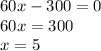
The derivative is negative to the left of
 and positive to the right of it, therefore, at
and positive to the right of it, therefore, at
 there exists the minimum.
there exists the minimum.
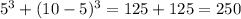
Therefore, the minimum value is 250.