Question

Use the taylor series expansion with the gamma lorentz factor: γ = 1/(1 – v^2/c^2)1/2

Answer 1

The Taylor series expansion is a mathematical representation of a function as an infinite sum of terms, where each term is calculated based on the derivatives of the function at a specific point.

To derive the Taylor series expansion of the gamma (γ) Lorentz factor, we can start by finding the derivatives of γ with respect to v.

Let's denote γ as a function of v:

γ(v) =
`1 / \sqrt(1 - v^2/c^2)`

To find the Taylor series expansion of γ(v), we need to calculate its derivatives with respect to v. We can use the chain rule for differentiation to simplify the process.

1st derivative:

γ'(v) =
`(-1/2) (1 - v^2/c^2)^(-3/2) (-2v/c^2) = v / (c^2 \sqrt(1 - v^2/c^2))^3`

2nd derivative:

γ''(v) =

`[1 / (c^2 * \sqrt(1 - v^2/c^2))^3]' * v + v * [1 / (c^2 * \sqrt(1 - v^2/c^2))^3]' \\= [(v / (c^2 * \sqrt(1 - v^2/c^2))^3]' * v + v * [1 / (c^2 *\sqrt (1 - v^2/c^2))^3]' \\= [3v / (c^2 *\sqrt(1 - v^2/c^2))^4] * v + v * [3v / (c^2 * \sqrt(1 - v^2/c^2))^4] \\ = 3v^2 / (c^2 * \sqrt(1 - v^2/c^2))^4`

We can observe a pattern in the derivatives, where the nth derivative can be written as:

γ^(n)(v) =
`(n * (n - 1) * ... * 3 * v^(n - 1)) / (c^2 * \sqrt(1 - v^2/c^2))^(n + 2)\\`

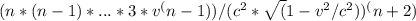
Now, we can write the Taylor series expansion for γ(v) centered at v = 0. Assuming c is a constant, we have:

γ(v) = γ(0) + γ'(0) * v + (γ''(0) / 2!) * v^2 + (γ'''(0) / 3!) * v³ + ...

Substituting the derivatives we derived earlier:

γ(v) = γ(0) + v / c² + (3v² / 2c²) + (3v²/ 2c⁶) + ...

The terms after the second term are higher-order terms representing the contributions of higher-order derivatives.

Note: The Taylor series expansion of γ(v) assumes that the function can be represented as a power series, which may not be valid for all functions. The validity and convergence of the series depend on the function and the range of values for which it is defined.