Question

Find the ordered pair solutions for the

system of equations.
f(x)=x²-3x - 10
f(x) = -x-2
([ ? ],
) and (
Enter the smallest x first.

Answer 1

`( - 2, 0 )\; and \; ( 4, - 6)`

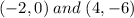
Explanation:

To find the ordered pairs set the right side expressions equal to each other and solve for x, then use those values for x to evaluate f(x) values

We get

x² - 3x - 10 = -x - 2

Moving -x - 2 to the left side gives

x² -3x - 10 + x + 2 = 0
(moving an expression from one side to another changes the signs of the terms)

Grouping like terms:
x² - 3x + x -10 +2 = 0

x² -2x -8 = 0

Expression on the left can be factored as (x + 2)(x-4)

This results in
(x + 2)(x - 4) = 0 giving

(x + 2) = 0 ==> x = -2 as one solution for x

(x - 4) =0 ==> x = 4 as the second solution

Plug in x = -2 into the second expression -x - 2 to get

f(-2) = -(-2) -2 = 2 - 2 = 0

So one ordered pair is (-2, 0)

Plug in x = 4 into -x - 2 to get
f(4) = - 4 -2 = -6

So (4, -6) is another ordered pair