Answer:
Wavelength:
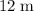 .
.
Period:
 .
.
Frequency:
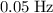 .
.
Amplitude:
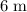 .
.
Step-by-step explanation:
In a wave, a crest is a point where displacement is the most positive. A trough is a point where displacement is the most negative.
Refer to the diagram attached. At the moment, boat A is at a "peak", meaning that it is currently at a crest of the wave. Boat B is a a "low point", meaning that it is at a trough of the wave.
The wavelength
 of a wave is the distance between two adjacent crests. Likewise, the distance between a crest and a neighboring trough would be
of a wave is the distance between two adjacent crests. Likewise, the distance between a crest and a neighboring trough would be
 . The question also stated that there is exactly one crest between the two boats.
. The question also stated that there is exactly one crest between the two boats.
It is given that the horizontal distance between boat A and boat B is
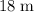 . This distance is equal to the sum of:
. This distance is equal to the sum of:
- distance between two crests,
 , (boat A, and the crest in between), and
, (boat A, and the crest in between), and - distance between a crest and a trough,
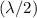 , (the crest in between, and boat B.)
, (the crest in between, and boat B.)
In other words:
 .
.
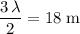 .
.
 .
.
Thus, the wavelength of this wave is
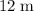 .
.
The period
 of a wave is the time it takes to complete one full cycle, which is
of a wave is the time it takes to complete one full cycle, which is
 in this question.
in this question.
The frequency
 of a wave is the number of cycles completed in unit time. Additionally,
of a wave is the number of cycles completed in unit time. Additionally,
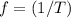 . In this question:
. In this question:
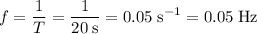 .
.
The amplitude
 of a wave is the maximum displacement of any given point on the wave relative to the equilibrium position.
of a wave is the maximum displacement of any given point on the wave relative to the equilibrium position.
The vertical distance between the crest and the equilibrium position is equal to amplitude
 . The vertical distance between a trough and the equilibrium position is also equal to
. The vertical distance between a trough and the equilibrium position is also equal to
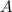 . As a result, the vertical distance between a crest and a trough would be
. As a result, the vertical distance between a crest and a trough would be
 .
.
In this question, it is given that the maximum vertical distance between the two boats is
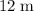 . This distance is achieved when one boat is at a crest and the other is at a trough. The distance between the two boats would then be
. This distance is achieved when one boat is at a crest and the other is at a trough. The distance between the two boats would then be
 .
.
Thus,
 . Hence, the amplitude of this wave would be:
. Hence, the amplitude of this wave would be:
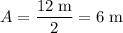 .
.