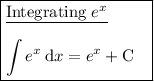Question

Evaluate the integral

Answer 1

`\textsf{C.} \quad (4^x)/(\ln 4)+C`

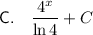
Explanation:

Given indefinite integral:

`\displaystyle \int 4^(2x)4^(-x) \; \text{d}x`

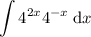
First, simplify the function by applying the exponent rule
`a^b \cdot a^c=a^(b+c)` :

`\begin{aligned}\displaystyle \int 4^(2x)4^(-x) \; \text{d}x&=\int 4^((2x+(-x)))\; \text{d}x\\\\&=\int 4^x\; \text{d}x\end{aligned}`

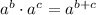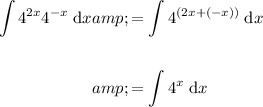
Rewrite 4 as
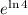`e^(\ln 4)`, therefore:

`\displaystyle \\=\int \left(e^(\ln 4)\right)^x\; \text{d}x`

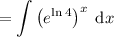
Apply the exponent rule
`(a^b)^c=a^(bc)`:

`\displaystyle =\int e^(x\ln 4)\; \text{d}x`

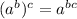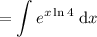
Now we can solve by substitution.

`\begin{aligned}\textsf{Let}\;\;u=x \ln 4 \implies \frac{\text{d}u}{\text{d}x}&=\ln 4\\\\ \implies \text{d}x&=(1)/(\ln 4)\;\text{d}u\end{aligned}`

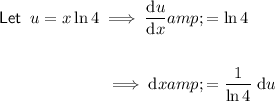
Rewrite the integral in terms of u and du.

`\displaystyle \int e^(x\ln 4)\; \text{d}x=\int e^u \cdot (1)/(\ln 4)\;\text{d}u`

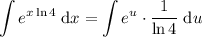
Take the constant outside the integral:

`\displaystyle=(1)/(\ln 4) \int e^u \;\text{d}u`

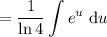
Integrate:

`\displaystyle =(e^u)/(\ln 4)+C`

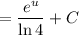
Substitute back in u = x ln 4:

`\displaystyle =(e^(x\ln 4))/(\ln 4)+C`

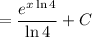
Apply the exponent rule
`(a^b)^c=a^(bc)`:

`\displaystyle =(4^x)/(\ln 4)+C`

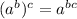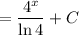
Therefore:

`\displaystyle \int 4^(2x)4^(-x) \; \text{d}x=(4^x)/(\ln 4)+C`

`\hrulefill`

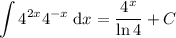
Integration rule used:

`\boxed{\begin{minipage}{3 cm}\underline{Integrating $e^x$}\\\\$\displaystyle \int e^x\:\text{d}x=e^x+\text{C}$\end{minipage}}`