Question

NO LINKS!! URGENT HELP!!!!!

Write a rule for the nth term of the geometric sequence. Then find a_9.

13. 7, -35, 175, -875, . . .
14. 104, -52, 26, -13, . . .

Answer 1

`\textsf{13.} \quad a_9 = 2734375`

`\textsf{14.} \quad a_9 = (13)/(32)`

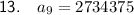
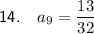
Explanation:

To write a rule for the nth term of a geometric sequence, we can use the following formula:

`\boxed{\begin{minipage}{5.5 cm}\underline{Geometric sequence}\\\\$a_n=ar^(n-1)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\\phantom{ww}$\bullet$ $r$ is the common ratio.\\\phantom{ww}$\bullet$ $a_n$ is the $n$th term.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

`\hrulefill`

Question 13

Given geometric sequence:

• 7, -35, 175, -875, ...

The first term is 7, so a = 7.

To find the common ratio, divide any term in the sequence by its preceding term:

`r=(-35)/(7)=-5`

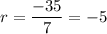
Therefore, the equation to find the nth term of the given geometric sequence is:

`\boxed{a_n=7(-5)^(n-1)}`

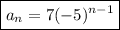
To find a₉, substitute n = 9 into the equation:

`\begin{aligned}a_9&=7(-5)^(9-1)\\&=7(-5)^8\\&=7(390625)\\&=2734375\end{aligned}`

Therefore, the 9th term of the given geometric sequence is 2,734,375.

`\hrulefill`

Question 14

Given geometric sequence:

• 104, -52, 26, -13, ...

The first term is 104, so a = 104.

To find the common ratio, divide any term in the sequence by its preceding term:

`r=(-52)/(104)=-(1)/(2)`

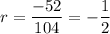
Therefore, the equation to find the nth term of the given geometric sequence is:

`\boxed{a_n=104\left(-(1)/(2)\right)^(n-1)}`

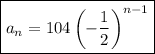
To find a₉, substitute n = 9 into the equation:

`\begin{aligned}a_9&=104\left(-(1)/(2)\right)^(9-1)\\\\&=104\left(-(1)/(2)\right)^(8)\\\\&=104\left((1)/(256)\right)\\\\&=(13)/(32)\end{aligned}`

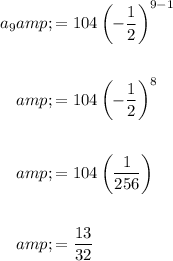
Therefore, the 9th term of the given geometric sequence is 13/32.