Question

The lengths of two sides of a triangle are shown.

Side 1: 3x² - 4x-1
Side 2: 4x-x² + 5
The perimeter of the triangle is 5x³ - 2x² + 3x - 8.
Part A: What is the total length of the two sides, 1 and 2, of the triangle? Show your work. (4 points)
Part B: What is the length of the third side of the triangle? Show your work. (4 points)
Part C: Do the answers for Part A and Part B show that the polynomials are closed under addition and subtraction? Justify your answer. (2 points)

Answer 1

`\textsf{A)} \quad 2x^2+4`

`\textsf{B)} \quad 5x^3-4x^2+3x-12`

`\textsf{C)} \quad \textsf{Yes - See below.}`

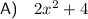
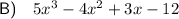
Explanation:

Part A

The lengths of two sides of a triangle are:

• Side 1: 3x² - 4x - 1
• Side 2: 4x - x² + 5

To find the total length of the two sides, Side 1 and Side 2, simply add them together:

`\begin{aligned}\sf Total\;length&=\sf Side\;1+Side\;2\\&=(3x^2-4x-1)+(4x-x^2+5)\\&=3x^2-4x-1+4x-x^2+5\\&=3x^2-x^2+4x-4x+5-1\\&=2x^2+4\end{aligned}`

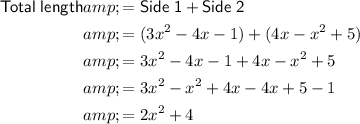
Therefore, the total length of Side 1 and Side 2 is:

`\Large\boxed{\boxed{2x^2+4}}`

`\hrulefill`

Part B

To find the length of the third side of the triangle, subtract the total length of the two given sides (from Part A) from the given perimeter:

`\begin{aligned}\sf Third\;side\;length&=\sf Perimeter-(Side\;1+Side\;2)\\&=(5x^3-2x^2+3x-8)-(2x^2+4)\\&=5x^3-2x^2+3x-8-2x^2-4\\&=5x^3-2x^2-2x^2+3x-8-4\\&=5x^3-4x^2+3x-12\end{aligned}`

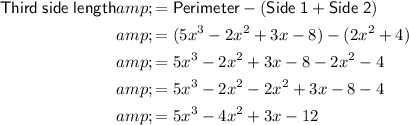
Therefore, the total length of Side 1 and Side 2 is:

`\Large\boxed{\boxed{5x^3-4x^2+3x-12}}`

`\hrulefill`

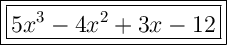
Part C

In Part A, when we added the polynomial expressions for Side 1 and Side 2, we obtained a new polynomial expression (2x² + 4).

In Part B, when we subtracted the total length of sides 1 and 2 from the given perimeter, we also obtained a new polynomial expression (5x³ - 4x² + 3x - 12).

For polynomials, being "closed" under addition means that if you add two polynomials together, the result will still be a polynomial. Similarly, being "closed" under subtraction means that if you subtract two polynomials, the result will also be a polynomial.

Therefore, as the addition and subtraction of polynomials in Part A and Part B resulted in new polynomial expressions, this demonstrates that the polynomials are closed under addition and subtraction.