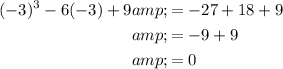Question

Helpppppp pleaseeeee​

Answer 1

`x^2+\left(b^3-3bc\right)x+c^3=0`

`\alpha = 1 \quad \textsf{and} \quad \beta=2`

`b=-3`

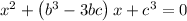
Explanation:

If α and β are roots of x² + bx + c = 0 then the equation must be:

`(x -\alpha)(x - \beta) = 0`

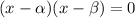
Expanding we get:

`x^2-\beta x - \alpha x + \alpha \beta = 0`

`x^2-(\alpha +\beta ) x + \alpha \beta = 0`

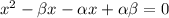
Equating the coefficients we get:

`\alpha + \beta=-b`

`\alpha \cdot \beta=c`

For an equation with the roots α³ and β³, the sum of the roots can be rewritten in terms of (α + β) and (α·β) using the Sum of Cubes formula, and the Square of Binomials formula:

`\begin{aligned}\alpha^3+\beta^3&=(\alpha + \beta)(\alpha^2-\alpha\beta+\beta^2)\\&=(\alpha + \beta)(\alpha^2+2\alpha\beta+\beta^2-3\alpha\beta)\\&=(\alpha + \beta)((\alpha+\beta)^2-3\alpha\beta))\end{aligned}`

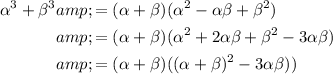
Substitute in the expressions for (α + β) and αβ to find the sum of the roots α³ and β³ in terms of b and c:

`\begin{aligned}\alpha^3+\beta^3&=(\alpha + \beta)((\alpha+\beta)^2-3\alpha\beta))\\&=(-b)((-b)^2-3c))\\&=-b(b^2-3c)\\&=-b^3+3bc\end{aligned}`

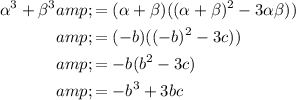
The product of the roots α³ and β³ in terms of c is:

`\alpha \cdot \beta = c`

`(\alpha \cdot \beta)^3 = c^3`

`\alpha^3 \cdot \beta^3=c^3`

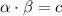
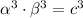
For a quadratic equation in the form x² + bx + c = 0:

• The sum of the roots is equal to -b.
• The product of the roots is equal to c.

So for x² + bx + c = 0 with roots α³ and β³:

`x^2-(\alpha^3 + \beta^3)x+(\alpha^3 \cdot \beta^3)=0`

`x^2-\left(-b^3-3bc\right)x+c^3=0`

`x^2+\left(b^3-3bc\right)x+c^3=0`

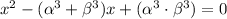
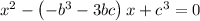
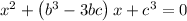
Therefore, the equation with the roots α³ and β³ is:

`\boxed{x^2+\left(b^3-3bc\right)x+c^3=0}`

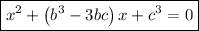
Substitute the given value of c = 2:

`x^2+\left(b^3-3b(2)\right)x+2^3=0`

`x^2+\left(b^3-6b\right)x+8=0`

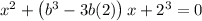
If b³ - 6b + 9 = 0, then (b³ - 6b) = -9.

Substitute this into the equation:

`x^2-9x+8=0`

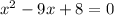
Factor:

`(x-1)(x-8)=0`

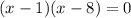
Therefore, the roots of the equation with the roots α³ and β³ are 1 and 8, so the values of α and β are:

`\alpha^3 =1 \implies \alpha = 1`

`\beta^3=8 \implies \beta=2`

To find the real roots of b³ - 6b + 9 = 0, substitute the found values of α and β into the expression for b:

`b=-(\alpha + \beta)`

`b=-(1+2)`

`b=-3`

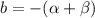
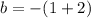
Therefore, the real root of b³ - 6b + 9 = 0 is b = -3.

We can confirm this by substituting b = -3 into the equation:

`\begin{aligned}(-3)^3-6(-3)+9&=-27+18+9\\&=-9+9\\&=0\end{aligned}`