Question

Evaluate the integral
guys pls help thank you sm

Answer 1

`\textsf{A.}\quad(1)/(3) \ln \left|\sec(3x+1)+\tan(3x+1)\right|+\text{C}`

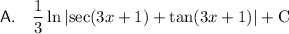
Explanation:

Fundamental Theorem of Calculus

`\displaystyle \int \text{f}(x)\:\text{d}x=\text{F}(x)+\text{C} \iff \text{f}(x)=\frac{\text{d}}{\text{d}x}(\text{F}(x))`

If differentiating takes you from one function to another, then integrating the second function will take you back to the first with a constant of integration.

Given integral:

`\displaystyle \int \sec(3x+1)\; \text{d}x`

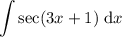
To evaluate the given integral, use the method of integration by substitution.

Let u = 3x + 1.

Find du/dx and rewrite it so that dx is on its own:

`\frac{\text{d}u}{\text{d}x}=3 \implies \text{d}x=(1)/(3)\;\text{d}u`

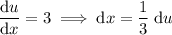
Rewrite the original integral in terms of u and du and integrate:

`\begin{aligned}\displaystyle \int \sec(3x+1)\; \text{d}x&=\int (1)/(3) \sec(u)\; \text{d}u\\\\&= (1)/(3)\int \sec(u)\; \text{d}u\\\\&= (1)/(3) \ln \left|\sec(u)+\tan(u)\right|+\text{C}\end{aligned}`

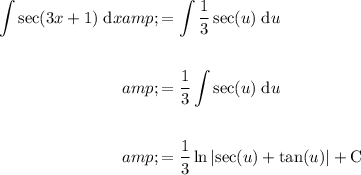
Finally, replace u with the original substitution.

`(1)/(3) \ln \left|\sec(3x+1)+\tan(3x+1)\right|+\text{C}`