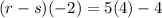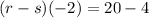Question

Suppose that the functions r and s are defined for all real numbers x as follows

r(x) = 5x ^ 2

s(x) = x ^ 3

Write the expressions for (rs)(x) and (r + s)(x) and evaluate (r - s)(- 2)

(rs)(x) =

(r + s)(x) =

(t - 5)(- 2) =

Answer 1

`(rs)(x)=5x^{5`

`(r+s)(x)=x^(2) (5+x)`

`(r-s)(-2)=16`

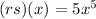
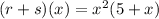
Explanation:

(rs)(x)= is going to be multiplying the two functions.

`(rs)(x)=(5x^(2))(x^(3))`

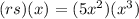
Add the exponents and get rid of the parentheses.

`(rs)(x)=5x^{5`

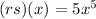
(r+s)(x)= is going to be adding the two functions.

`(r+s)(x)=5x^(2) +x^(3)`

Factor out any common factors.

`(r+s)(x)=x^(2) (5+x)`

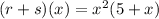
(r-s)(-2)= is going to be subtracting the functions from each other while evaluating -2 into the problem.

`(r-s)(-2)=5(-2)^(2) -(-2)^(2)`

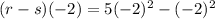
Solve.

`(r-s)(-2)=5(4) -4`

`(r-s)(-2)=20 -4`

`(r-s)(-2)=16`