Question

Please help you guys, the AP calc an exam coming soon and I need to know how to do this, much appreciated.

Answer 1

To be continuous at x=0, you need three things:

1. f(0) must be defined

2. limit as x –> 0 must exist

3. f(0) = limit as x –> 0

f(0) in this case is the following:

`f(0) = k + 2 \ln(0+e^(0+1)) = k + 2 \ln(e) = k + 2`

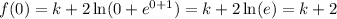
We have to pause on this, since this by itself cannot give us the value of k.

For the limit, you need to make sure the limit from the left matches the limit from the right.

`\lim\limits_(x\to 0^+) k+2\ln(x+e^(x+1)) = k+2`

`\lim\limits_(x\to 0^-) (\sin(7x))/(2x) =(7)/(2)`

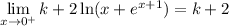
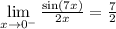
The only way this limit can exist is if
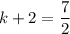`k+2 = (7)/(2)`, which means
`k = (3)/(2)`.

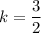Using that k-value also allows f(0) = 7/2, which makes your function continuous.

If you need to know how to make that second limit work out to 7/2, there are two steps to take.

The first is to bring the 1/2 out front, since it's a constant factor inside the limit.

`\lim\limits_(x\to 0^-) (\sin(7x))/(2x) =(1)/(2)\cdot\lim\limits_(x\to 0^-) (\sin(7x))/(x)`

The second is to manipulate the what you're taking the limit of to turn it into a "sin(u)/u" situation. To do this, we'll multiply by 7/7 inside the limit:

`(1)/(2)\cdot\lim\limits_(x\to 0^-) (\sin(7x))/(x)=(1)/(2)\cdot\lim\limits_(x\to 0^-) \frac{{\boldsymbol7\cdot{}}\sin(7x)}{{\boldsymbol7\cdot{}}x}`

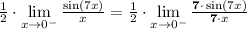
We'll then factor out the 7 in the numerator like we did with the 1/2:

`=(7)/(2)\cdot\lim\limits_(x\to 0^-) (\sin(7x))/(7x)`

And now with a quick u-substitution, we'll let u = 7x and x->0 is the same as u->0, we have

`=(7)/(2)\cdot\lim\limits_(u\to 0^-) (\sin(u))/(u)`

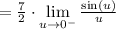
This is useful because a good limit to know in calculus is that
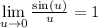`\lim\limits_(u\to 0) (\sin(u))/(u)=1`.