Question

Rory currently has $1200 saved in his bank account. In 8 years, Rory will be 32 years old and have $1580.17 saved in his bank account.

A: Write an exponential equation in the form y=ab^x that represents Rory's bank account x years from now if the interest rate remains the same. Round values to 3 decimal places, if necessary.
B: How much can Rory expect to have in his bank account when he is 50 years old?
C: How much can Rory expect to have in his bank account if he lived to be 100 years old?

Answer 1

`\textsf{A)} \quad y=1200\cdot 1.035^x`

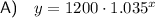
B) $2,935.15

C) $16,392.60

Explanation:

The general form of an exponential function is:

`\boxed{y=ab^x}`

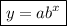
where:

• a is the initial value.
• b is the base (growth/decay factor) in decimal form.

Given:

• y is the account balance (in dollars).
• x is the number of years from now.

If Rory currently has $1,200 saved in his bank account, then the initial value is a = 1200.

If in 8 years time, the account balance will be $1,580.17, then y = 1580.17 when x = 8.

Substitute x = 8, y = 1580.17 and a = 1200 into the exponential function and solve for b:

`\begin{aligned}y&=ab^x\\\\\implies 1580.17&=1200 \cdot b^8\\\\(1580.17)/(1200)&=b^8\\\\\sqrt[8]{(1580.17)/(1200)}&=b\\\\b&=1.03499993...\\\\b&=1.035\; \sf (3\;d.p.)\end{aligned}`

Therefore, the exponential equation that represents Rory's bank account x years from now if the interest rate remains the same is:

`\boxed{y=1200\cdot 1.035^x}`

`\hrulefill`

Part B

If 8 years from now Rory will be 32 years old, then he is currently 24 years old, since 32 - 8 = 24.

To calculate how much Rory can expect to have in his bank account when he is 50 years old, substitute x = 26 into the equation created in Part A, since 50 - 24 = 26.

`\begin{aligned}y&=1200 \cdot 1.035^(26)\\y&=2935.1502...\end{aligned}`

Therefore, Rory can expect to have $2,935.15 in his bank account when he is 50 years old.

`\hrulefill`

Part C

To calculate how much Rory can expect to have in his bank account when he is 100 years old, substitute x = 76 into the equation created in Part A, since 100 - 24 = 76.

`\begin{aligned}y&=1200 \cdot 1.035^(76)\\y&=16392.5995...\end{aligned}`

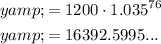
Therefore, Rory can expect to have $16,392.60 in his bank account when he is 100 years old.