Question

Two men are standing on the same side of 100m high tower measure of the angles of elevation of the top of the tower are 20 and 30° respectively. Find the distance between them

Solve with diagram ​

Answer 1

101.5 m

Explanation:

Let man 1 be the man whose angle of elevation is 30°.

Let man 2 be the man whose angle of elevation is 20°.

We can model the given scenario as a right triangle with the height of the tower as the triangle's height (100 m), and the distance between the base of the tower and man 2 as the base of the triangle.

As the angle of elevation for man 1 is greater than the angle of elevation for man 2, the position of man 1 is between the base of the tower and man 2.

Let "a" be the distance between man 1 and the base of the tower.

Let "b" be the distance between man 2 and the base of the tower.

Therefore, we have 2 right triangles (see attached diagram):

• Triangle 1 has an angle of elevation of 30°. The side opposite the angle is 100 m and the side adjacent the angle is labelled "a".
• Triangle 2 has an angle of elevation of 20°. The side opposite the angle is 100 m and the side adjacent the angle is labelled "b".

The distance between the two men is b - a.

We can calculate the values of a and b by using the tangent trigonometric ratio, since we have the side opposite the angle and wish to find the side adjacent the angle.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

Using the tan ratio, create an equation for a:

`\tan 30^(\circ)=(100)/(a)`

`a=(100)/(\tan 30^(\circ))`

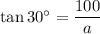
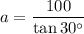
Using the tan ratio, create an equation for b:

`\tan 20^(\circ)=(100)/(b)`

`b=(100)/(\tan 20^(\circ))`

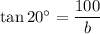
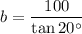
As the distance between the two men is b - a:

`\begin{aligned}\textsf{Distance between the men}&=b-a\\\\&=(100)/(\tan 20^(\circ))-(100)/(\tan 30^(\circ))\\\\& = 274.747741...-173.205080...\\\\&=101.542661...\\\\&=101.5\; \sf m\;(nearest\;tenth)\end{aligned}`

Therefore, the distance between the two men is 101.5 meters, to the nearest tenth.