Question

The hypotenuse of a right-angled triangle has a length of 11 cm. One of the shorter sides

has a length of 7 cm. What is the value of the third side?

Answer 1

6√3

Explanation:

solution:

given

hypotenuse(h)=11cm

perpendicular(p)=7 cm

base(b)=?

we know that,

h²=p² +b²

11²=7²+b²

121=49+b²

121-49=b²

72=b²

√72=b

6√3=b

Answer 2

Answer: b = 6
`√(2)`

Explanation:

We can use the Pythagorean theorem where c is the hypotenuse and a and b are the legs (shorter sides).

Given:

a² + b² = c²

Substitute known values:

(7)² + b² = (11)²

Square:

49 + b² = 121

Subtract both sides of the equation by 49:

b² = 72

Take the square root of both sides of the equation:

➜ We cannot have a negative side length here, so we will take only the positive root.

b =
`√(72)`

Simplify:

b =
`√(36*2)`

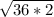
b = 6
`√(2)`