Question

Enter values to write the function that matches the graph shown.

Answer 1

`k(x) = (x + 1) (4x + 16)\\`

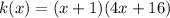
Explanation:

The equation of a parabola given roots
`x_1` and
`x_2` is

`y = a( x - x_1)(x - x_2)`

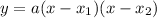
where a is a constant

The x-intercepts of a parabola will be the roots of the quadratic equation to the parabola since k(x) = 0 at these points

The x-intercepts are (-1, 0) and (-4, 0)

Therefore the equation of the parabola is of the form

`k(x) = a ( x - (-1) ) ( x - (-4) )`

`= a( x+ 1) (x + 4)`

To find a, find a point (x, y) through which the parabola passes and plug this value into the above equation to solve for a

We see that the parabola passes through (-5, 16) and (0, 16). The latter point is also the y-intercept of the parabola

This means k(x) = 16 at x = 0

Plugging (0, 16) into the equation gives

`k(x) = a(x + 1) ( x + 4)`

`a(x + 1) ( x+ 4) = k(x)`

`a(0 + 1) (0 + 4) = 16`

`a \cdot 1 \cdot 4 = 16`

`4a = 16`

`a = 16/4 = 4`

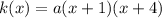
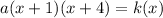
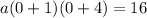
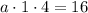
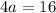
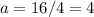
Equation of the parabola is

`k(x) = 4 (x + 1) (x + 4)`

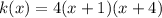
which can be rewritten as