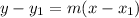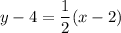Answer:
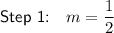
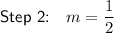
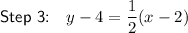
Explanation:
Given linear equation:
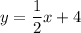
The given equation is in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.
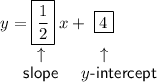
Therefore, the slope of the given line is:
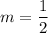
We are told that the new line is parallel to the given line.
Since parallel lines have the same slope, the slope of the new line is the same as the slope of the given line:
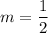
We are told that the new line passes through the point (2, 4).
Therefore, we can plug in the found slope, m = 1/2, and the given point (2, 4), into the point-slope form: