Question

NO LINKS!! URGENT HELP PLEASE!!

6. Anisha invested $8000 in an account that earns 10% interest. How much money will she have in 15% in the interest is compounded quarterly?


7. Kevin borrowed $32,500 to purchase a new car. If the rate on the loan is 6% compounded annually, how much will he pay in total oer the course of the 5 year loan?

Answer 1

6) $35,198.32

7) $43,492.33

Explanation:

To solve both these problems, we can use the formula for compound interest:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Question 6

Given values:

• P = $8,000
• r = 10% = 0.1
• n = 4 (quarterly)
• t = 15 years

Substitute the given values into the formula and solve for A:

`A=8000\left(1+(0.1)/(4)\right)^(4\cdot 15)`

`A=8000\left(1+0.025\right)^(60)`

`A=8000\left(1.025\right)^(60)`

`A=35198.3179905`

`A=35198.32`

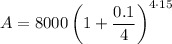
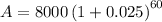
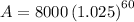
Therefore, the balance of Anisha's account after 15 years will be $35,198.32.

`\hrulefill`

Question 7

Given values:

• P = $32,500
• r = 6% = 0.06
• n = 1 (annually)
• t = 5 years

Substitute the given values into the formula and solve for A:

`A=32500\left(1+(0.06)/(1)\right)^(1\cdot 5)`

`A=32500\left(1+0.06\right)^(5)`

`A=32500\left(1.06\right)^(5)`

`A=43492.331272`

`A=43492.33`

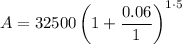
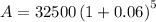
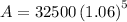
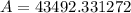
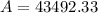
Therefore, Kevin will pay a total of $43,492.33 over the course of the 5 year loan (assuming he doesn't pay any of the loan back over those 5 years).