Question

What is the value of the geometric series?

Answer 1

2728

Explanation:

Sigma notation is a concise way to represent a series. It is denoted by the Greek capital letter, ∑, which represents the sum.

Given geometric series (sigma notation):

`\displaystyle \sum^(7)_(k=3)\left((1)/(2) \cdot 4^(k-1)\right)`

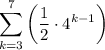
The variable k is the index of summation.

`\textsf{First value of $k$:} \quad k = 3`

`\textsf{Last value of $k$:} \quad k = 7`

`\textsf{Formula for each term in the sequence:} \quad a_k=(1)/(2) \cdot 4^(k-1)`

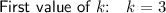
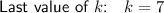
To generate the terms of a series expressed in sigma notation, substitute the index of summation, k, with consecutive integers from the first value to the last value of the index.

`\begin{aligned}\displaystyle\sum^(7)_(k=3)\left(\frac12 \cdot4^(k-1)\right)&=\left(\frac12\cdot4^(3-1)\right)+\left(\frac12\cdot4^(4-1)\right)+\left(\frac12\cdot4^(5-1)\right)+\left(\frac12\cdot4^(6-1)\right)+\left(\frac12\cdot4^(7-1)\right)\\\\&=\left(\frac12\cdot4^2\right)+\left(\frac12\cdot4^3\right)+\left(\frac12\cdot4^4\right)+\left(\frac12\cdot4^5\right)+\left(\frac12\cdot4^6\right)\end{aligned}`

`\begin{aligned}&=\left(\frac12\cdot16\right)+\left(\frac12\cdot64\right)+\left(\frac12\cdot256\right)+\left(\frac12\cdot1024\right)+\left(\frac12\cdot4096\right)\\\\&=8+32+128+512+2048\\\\&=2728\end{aligned}`

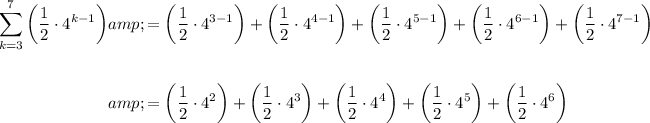
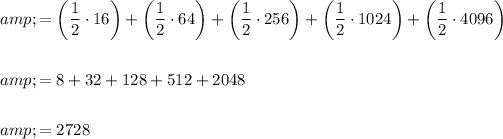
Therefore, the value of the geometric series is 2728.