Question

Find the reference angles and quadrant/angles of 2secx-1 = secx+3?

Answer 1

Reference angle: x = 75.52° + 360°n (2 d.p.)

Quadrant IV angle: x = 284.48° + 360°n (2 d.p.)

Explanation:

A reference angle is the acute angle that is formed between the terminal side of an angle and the x-axis. Its vertex is at the origin and it is always positive irrespective of which side of the axis it is falling.

Quadrant angles are the angles that lie within each of the four quadrants in a coordinate plane. They can be classified based on the quadrant in which their terminal side resides.

Reference angles are useful in trigonometry because the values of the trigonometric functions for an angle and its reference angle are the same, except for their signs, which depend on the quadrant in which the angle lies. Therefore, we can use the reference angle to simplify calculations involving trigonometric functions of angles in different quadrants.

To find the reference and quadrant angles of the given equation, first solve the equation for x.

`\begin{aligned}2 \sec x-1 &= \ sec x+3\\\\2 \sec x-1 - \sec x&= \ sec x+3- \sec x\\\\ \sec x-1 &= 3\\\\ \sec x-1+1 &= 3+1\\\\\sec x&=4\\\\(1)/(\cos x)&=4\\\\\cos x &=(1)/(4)\end{aligned}`

Use the inverse cosine function to determine the angle.

`\cos^(-1)\left((1)/(4)\right) =75.52^(\circ)\;\;(\sf 2\;d.p.)`

Therefore, the reference angle is 75.52°.

To find the quadrant angle, we need to consider the signs of cosine in each quadrant. The cosine function is positive in Quadrants I and IV.

Therefore, to find the second solution, subtract the reference angle from 360° to find the solution in Quadrant IV.

`360^(\circ)-75.52^(\circ)=284.48^(\circ)\;\; \sf (2 \; d.p.)`

Therefore, the solutions to the given equation are:

• x = 75.52° + 360°n (2 d.p.)
• x = 284.48° + 360°n (2 d.p.)

Answer 2

• To solve the equation 2sec(x) - 1 = sec(x) + 3,

we can begin by using the identity
`sec(x) = (1)/(cos(x))` and converting everything to terms of cosine.

First, we can simplify the equation by adding 1 to both sides:

2sec(x) = sec(x) + 4

Next, substituting sec(x) with 1/cos(x), we get:

2
`*(1)/(cos(x))` =
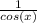`(1)/(cos(x))` + 4

Multiplying both sides by cos(x), we get:

2 = 1 + 4cos(x)

Subtracting 1 from both sides, we get:

1 = 4cos(x)

Dividing both sides by 4, we get:

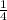`(1)/(4)` = cos(x)

Therefore, the reference angle of x is
`cos^(-1)(1)/(4)`, which is approximately 75.52 degrees.

• To find the quadrant/angles of x, we need to look at the sign of both sec(x) and cos(x). Since sec(x) =
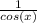  `(1)/(cos(x))`, if cos(x) is positive, then sec(x) is also positive, and vice versa.

From the equation
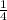`(1)/(4)` = cos(x), we know that cos(x) is positive, so sec(x) is also positive. This means that x is either in the first or fourth quadrant.

To determine the exact angle(s) in these quadrants, we can use the inverse trigonometric function arccos.

In the first quadrant, arccos(
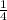`(1)/(4)`) is approximately 75.52 degrees.

In the fourth quadrant, the angle with the same reference angle is 360 - 75.52, which is approximately 284.48 degrees.

Therefore, the solutions for x are:

x = 75.52 degrees + n(360 degrees)

or

x = 284.48 degrees + n(360 degrees)

where n is an integer.