Correct statements are:
b.

c. The measure of the reference angle is
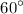 .
.
The measure of angle
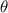 is
is
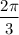 . This corresponds to a reference angle of
. This corresponds to a reference angle of
 because
because
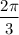 is in the second quadrant.
is in the second quadrant.
Now, let's evaluate each statement:
a.
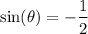
This is not true for
 ; the correct value is
; the correct value is
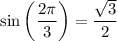 .
.
b.

This is true for
 .
.
c. The measure of the reference angle is
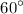 .
.
The reference angle is
 , which is equivalent to
, which is equivalent to
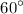 . This statement is true.
. This statement is true.
d. The measure of the reference angle is
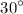 .
.
This is not true; the correct measure is
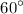 .
.
e. The measure of the reference angle is
 .
.
This is not true; the correct measure is
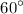 .
.
f.
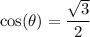
This is not true for
 ; the correct value is
; the correct value is
 .
.
Complete Question:
Select all the correct answers.
If the measure of angle
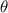 is
is
 , which statements are true?
, which statements are true?
a.
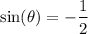
b.
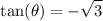
c. The measure of the reference angle is
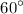 .
.
d. The measure of the reference angle is
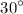 .
.
e. The measure of the reference angle is
 .
.
f.
