Question

What is the value of b? Help pls!!!

Answer 1

b=24

Explanation:

Main concepts

Concept 1. Congruent Triangles

Concept 2. Hypotenuse-Leg Congruence

Concept 3. Congruent Triangles implies congruent parts

Concept 4. Solving a one-variable equation

Concept 1. Congruent Triangles

For two triangles to be congruent, the three angles of one triangle must be congruent to the three angles of the other triangle, AND the three side lengths of one triangle must be congruent to the three side lengths of the other triangle.

Fortunately, through various proofs about different types of triangles, it isn't necessary to prove all six of those things.

The 5 cases of triangle Congruence are

1. SSS -- Side-Side-Side
2. SAS -- Side-Angle-Side
3. ASA -- Angle-Side-Angle
4. AAS -- Angle-Angle-Side
5. HL -- Hypotenuse-Leg (only for Right Triangles, since a Hypotenuse is a part of a Right Triangle)

Concept 2. Hypotenuse-Leg Congruence

Proving they are both right triangles, and that HL congruence can be used

In this situation, we are given that Angle UVT is a right angle. Under the assumption that US is a line that contains V, then Angle UVT and Angle SVT form a linear pair and are supplementary (their measures add to 180 degrees).

So, Angle SVT is also a right angle. This means that both Triangle UVT and Triangle SVT are Right Triangles, since they are each a triangle with a right angle.

To prove HL congruence, we need to prove that one leg of each triangle is congruent to the other, and that the hypotenuse of each triangle is congruent to the other.

Proving Hypotenuse congruence

Note that the Hypotenuse (side across from the right angle) of Triangle UVT is side UT with measure 67 units.

The Hypotenuse of Triangle SVT is side ST, also with measure 67 units.

So the Hypotenuses are congruent.

Proving Leg congruence

Note that one leg of the triangles is shared as a common side: line segment VT is common to both triangles. Even though we don't know the actual length of VT, the length of VT for the first triangle is the same as the length of VT for the second triangle.

The official reason that VT is congruent to VT is because of the "Reflexive property".

Since the Hypotenuses and one leg from each triangle are congruent, the two triangle are congruent. Specifically, Triangle UVT is congruent to Triangle SVT.

Concept 3. Congruent Triangles implies congruent parts

Even though we didn't prove all 6 congruences, we did prove that the triangles ARE congruent. Therefore, all 6 congruences are true. This means that any other pair of corresponding parts is also congruent.

Specifically, we're interested in the last pair of sides, because they have measurements that contain "b" the value we're trying to solve for.

Side UV is congruent to Side SV because Corresponding parts of Congruent triangles are Congruent.

This means that their lengths are equal:

`Length_(UV)=Length_(SV)`

`b+24=2b`

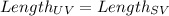
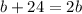
Concept 4. Solving a one-variable equation

For any equation in math where there is only one item that is unknown, (even if it shows up multiple times in the equation), there are two main steps:

Step 1. Get the variable to show up exactly once

Step 2. Isolate the variable

Step 1. Get the variable to show up exactly once

Since we know that in the very end, we want b=__, we know that the b will appear only once (and thus only on one side of the equation, not both), and will be by itself.

In practice, sometimes there are special tricks that have to be employed to make this step happen. Generally, this means simplify each side of the equation, and try to group like terms together.

For this equation, observe that b appears twice: once on the left side of the equation, and once on the right side of the equation.

At some point, we'll need to get the "b"s on the same side of the equation, and hopefully combine like terms into a single term with b.

To get the "b"s on one side, we'll subtract b from both sides:

`(b+24)-b=(2b)-b`

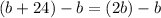
On the left, the positive b and negative b cancel completely, leaving just 24. On the right, the 2b subtracted by 1b leaves just 1b, or more simply, b.

`24=b`

Step 2. Isolate the variable

While trying to get the variable to show up exactly once, we also incidentally isolated the variable, as the like terms combined.

So, b=24.