Question

Find the volume of the prism. Show all your work.
20 cm.
2 cm.
4 cm.
16 cm.

Answer 1

V=128 cm^3

Explanation:

The volume formula for an oblique prism (slanted prism) is
`V=Bh`, where B is the area of the base, and h is the height of the prism aka the distance from the highest point furthest from the base along a line segment that is normal to ("normal" is the 3-d version of "perpendicular" ) the plane that contains the base.

Since the base is a rectangle, B=lw.

This modifies the formula for our oblique prism to be
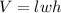`V=lwh`, which looks exactly like the formula for a standard rectangular prism
`V=lwh`.

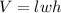A helpful visualization

Visualize a deck of playing cards (not in the box, but neatly organized into a pile). It is approximately a standard rectangular prism.

Now imagine shifting each card slightly to the right of the card below it, so that the pile is now slanted. The pile now looks like an oblique prism (although perhaps not as exaggerated as the prism we see here).

In both cases, the volume of space that the cards takes up is the same.

If the cards were shifted a little more, and a little more, even though the diagonal distance along the "slant" grows longer the more we spread those cards out, the "height" of the deck remains unchanged, and the area of the base (the area of the face of the bottom card) remains unchanged, and the total volume of the deck remains unchanged.

Calculating volume

So, the volume of this oblique prism is V=Bh, where the B is the area of the rectangle at the base (dimensions 2cm by 4cm), and the h is the height of 16 cm.

B = (2cm) * (4cm)

B = 8 cm^2

V = (8 cm^2) * (16cm)

V = 128 cm^3

Answer 2

Answer: 128 cm^3

Explanation:

Its the same as any other Prism

V = lwh

= 2x4x16

= 128 cm^3