Question

Need help urgently, don’t think the answers i have are right and i don’t know how to do it!!!

Answer 1

• See attached graph

• y-intercepts =
  `(3)/(2)`

• Roots: x = - 3
  
• Vertical asymptote: x = -2
  Horizontal asymptote y = 1

• End behavior
  
  `\mathrm{as}\:x\to \:+\infty \:,\:y\to \:1,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:y\to \:1`
  
• Table:
  x y
• -4 1/2
• - 3 0
• -1 2
• 0 3/2
• 1 4/3
• 2 5/4
• 3 6/5
• Note that the function is undefined at x = -2
• 
  

Explanation:

Given function is

`f(x) = (\left(x^2-9\right))/(\left(x^2-x-6\right))`

Part 1

Graph attached

y-intercepts can be found by finding f(0) ie the value of f(x) at x = 0

`f(0) = (\left(0^2-9\right))/(\left(0^2-0-6\right)) = (-9)/(-6) = (3)/(2)`

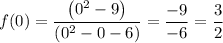
Roots of a function can be found by setting f(x) = 0 and solving for x

Setting f(x) = 0

==>
`(x^2-9)/(x^2-x-6) = 0\\\\`

We can factor the numerator as follows:
x² - 9 = (x + 3) (x -3) since (a + b)(a-b) = a² - b²

Denominator can be factored as follows
x² - x - 6 = (x-3)(x+2)

So

`f(x) = ((x + 3)(x-3))/((x-3)(x+2))\\\\`

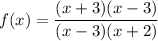
The (x-3) term cancels leaving

`f(x) = (x+3)/(x+2)`

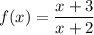
Setting this equal to 0 gives

`(x+3)/(x+2) = 0`

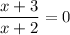
This is 0 when x + 3 = 0 or x = -3

So there is only one root and that is x = -3

Asymptotes

The vertical asymptote occurs when at a value of x when the denominator becomes 0

The given function has been factored as

`f(x) = (x + 3)/(x + 2)`

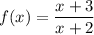
The denominator becomes 0 at x = -2
Vertical asymptote is x = - 2

To find the horizontal asymptote use the fact that when the degrees of the numerator and denominator are equal, the horizontal asymptote is given by

`y=\frac{\mathrm{numerator's\:leading\:coefficient}}{\mathrm{denominator's\:leading\:coefficient}}`

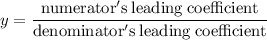
The degree of the numerator x + 3 is 1 and the degree of the denominator x + 2 is also 1

So the horizontal asymptote is y = 1/1 = 1

y = 1 is the horizontal asymptote

End behavior is the behavior of the function as x → ±∞

This is determined by examining the leading term of the function and determining what its behavior is as x → ±∞

In the function

`f(x) = (x + 3)/(x + 2)`
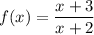
which is the factored form of the originally given function
the domain of x = all real numbers with the exception of -2 since at x = -2, the function is undefined

The end behavior can be determined by finding the limit of f(x) as x tends to infinity

`\lim _(x\to \infty \:)\left((x+3)/(x+2)\right)\\\\(x+3)/(x+2) \text{ can be transformed by dividing by x both numerator and denomiator :}\\\\\\=((x)/(x)+(3)/(x))/((x)/(x)+(2)/(x))\\\\\\=(1+(3)/(x))/(1+(2)/(x))`

`\lim _(x\to \infty \:)\left((x+3)/(x+2)\right) \\\\\\\\=\lim _(x\to \infty \:)\left((1+(3)/(x))/(1+(2)/(x))\right)\\\\\\\\=(\lim _(x\to \infty \:)\left(1+(3)/(x)\right))/(\lim _(x\to \infty \:)\left(1+(2)/(x)\right))`

`\lim _(x\to \infty \:)\left(1+(3)/(x)\right) = 1\\\\\lim _(x\to \infty \:)\left(1+(2)/(x)\right) = 1`

`\lim _(x\to \:-\infty \:)\left((x+3)/(x+2)\right) = 1`

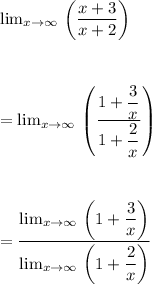
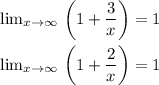
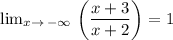
End behavior

`\mathrm{as}\:x\to \:+\infty \:,\:y\to \:1,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:y\to \:1`

Table:
x y

-4 1/2

- 3 0

-1 2

0 3/2

1 4/3

2 5/4

3 6/5

Note that the function is undefined at x = -2