The expressions for the reactance
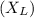 and the inductance
and the inductance
 in terms of
in terms of
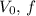 , and
, and
 are:
are:
1.
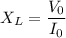
2.

The reactance of an inductor
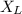 in an AC circuit is given by the formula:
in an AC circuit is given by the formula:
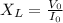
This formula relates the voltage across an inductor
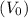 to the current flowing through it
to the current flowing through it
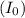 in an AC circuit.
in an AC circuit.
The inductive reactance
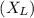 is also related to the inductance
is also related to the inductance
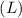 and frequency
and frequency
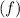 in the following way:
in the following way:
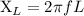
Now, we can use these formulas to derive the expressions for
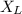 and
and
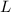 in terms of
in terms of
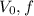 , and
, and
 :
:
From the first equation
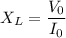 , we can rearrange to solve for
, we can rearrange to solve for
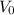 :
:
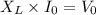
So, the expression for
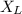 in terms of
in terms of
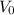 and
and
 is:
is:
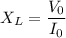
From the second equation
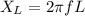 , we can rearrange to solve for
, we can rearrange to solve for
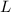 :
:
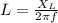
Substitute the expression for
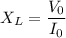 :
:

Substituting
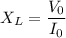 into the expression for inductance
into the expression for inductance
 :
:
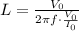
Now, let's simplify this expression:

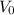 cancels out in the numerator and denominator:
cancels out in the numerator and denominator:
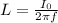
Therefore, after substitution, the expression for the inductance
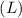 in terms of
in terms of
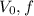 , and
, and
 simplifies to:
simplifies to:
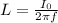
The complete question is given below:
An inductor is hooked up to an AC voltage source. The voltage source has EMF
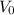 and frequency
and frequency
 . The current amplitude in the inductor is
. The current amplitude in the inductor is
 .
.
Part A
What is the reactance
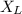 of the inductor?
of the inductor?
Express your answer in terms of V0 and
 .
.
Part B
What is the inductance
 of the inductor?
of the inductor?
Express your answer in terms of
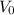 ,
,
 , and
, and
 .
.