When we are considering a random integer selected from the range from 2 to 10,000,000,000, there are 9,999,999,999 possible integers to choose from. Now, we need to determine how many of these integers are prime.
One way to approach this problem is to use the Prime Number Theorem, which states that the number of primes less than or equal to x is approximately x/ln(x). Using this theorem, we can estimate the number of primes less than or equal to 10,000,000,000 as:
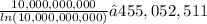
Therefore, there are approximately 455,052,511 prime numbers in the range from 2 to 10,000,000,000.
To find the probability of selecting a prime number, we need to divide the number of primes by the total number of integers in the range:
455,052,511/9,999,999,999 ≈ 0.0455
So, the chances of selecting a prime number from the range from 2 to 10,000,000,000 is approximately 0.0455 or 4.55%.
It is important to note that this is only an approximation based on the Prime Number Theorem and the actual number of primes in the range may differ slightly from this estimate. However, it gives us a good idea of the likelihood of selecting a prime number from this range.