Question

Need Help PLease Very Importatn giving 20 POINTS

Answer 1

The last option:
`3 x^{^{(9)/(2)}}y^{^{(3)/(2)}}`

Explanation:

Main concepts:

Concept 1. Parts of a Radical

Concept 2. Radicals as exponents

Concept 3. Exponent properties

Concept 4. How to simplify a radical

Concept 1. Parts of a Radical

Radicals have a few parts:

• the radical symbol itself,
• the "index" (the number in the little nook on the left), and
• the "radicand" (the part inside of the radical).

If the index isn't shown, it is the default index of "2". This default index for a radical represents a square root, which is why people sometimes erroneously call the radical symbol a square root even when the index is not 2.

In this situation, the radical's index is 4, and the radicand is 81 x^18 y^6.

Concept 2. Radicals as exponents

For any radical, the entire radical expression can be rewritten equivalently as the radicand raised to the power of the reciprocal of the index of the radical. In equation form:

`\sqrt[n]{x} =x^{^{(1)/(n)}}`

So, the original expression can be rewritten as follows:

`\sqrt[4]{81x^(18)y^(6)}`

`(81x^(18)y^(6))^{^{(1)/(4)}}`

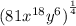
Concept 3. Exponent properties

There are a number of properties of exponents:

• Multiplying common bases --> Add exponents:
  `x^ax^b =x^(a+b)`
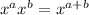
• Dividing common bases --> Subtract exponents:
  `(x^a)/(x^b) =x^(a-b)`

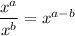
• Bases raised to powers, raised again to another power, multiplies powers:
  `(x^a)^b =x^(ab)`
• A "distributive" property for powers across multiplication (warning... does not work if there are ANY addition or subtractions):
  `(xy)^a =x^(a)y^(a)`

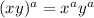
Continuing with our expression,
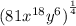`(81x^(18)y^(6))^{^{(1)/(4)}}`, we can apply the "distributive" property since all of the parts are multiplied to each other...

`(81)^{^{(1)/(4)}}(x^(18))^{^{(1)/(4)}}(y^(6))^{^{(1)/(4)}}`

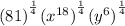
Applying the "Bases raised to powers, raised again to another power, multiplies powers" rule for the parts with x and y...

`(81)^{^{(1)/(4)}}(x^{^{(18)/(4)}})(y^{^{(6)/(4)}})`

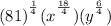
Reducing those fractions, (both the numerators and denominators have a factor of 2)...

`(81)^{^{(1)/(4)}}(x^{^{(9)/(2)}})(y^{^{(3)/(2)}})`

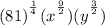
Rewriting the exponent of the "81" back as a radical...

`\sqrt[4]{81} x^{^{(9)/(2)}}y^{^{(3)/(2)}}`

Concept 4. How to simplify a radical

For any radical with index "n", the result is the number (or expression) that when multiplied together "n" times gives the radicand.

In our case, the index is 4. So, we're looking for a number that when multiplied together four times, gives a result of 81.

One method of simplifying radicals is to completely factor the radicand into prime factors, and forms groups (each containing an "n" number of matching items).

Note that 81 factors into 9*9, which further factors into 3*3*3*3

This is a group of 4 matching items, and since the index of the radical is 4, we have found a group that can be factored out of the radical completely:

`\sqrt[4]{81} =\sqrt[4]{(3*3*3*3)}=3`

So, our original expression, simplifies finally to
`3 x^{^{(9)/(2)}}y^{^{(3)/(2)}}`

This is the last option for the multiple choice.