Question

A cylinder has a height of 8 feet and a diameter of 12 feet. Which of the following is a true statement?

A- All of the answers listed
B- A cone with the same height and radius would have a volume of 96π ft³
C- The volume of the cylinder is 288π ft³
D- The area of the base is 36π ft²

Answer 1

A- All of the answers listed

Explanation:

Let's consider each choices:-

B- A cone with the same height and radius would have a volume of 96π ft³.

In this case, we are replaced with the cone figure that has diameter of 12 feet and height of 8 feet. We know that the formula of cone's volume is:

`\displaystyle{(1)/(3)\pi r^2 h}`

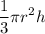
Our radius is half of diameter which is 12/2 = 6 feet. Therefore:

`\displaystyle{V = (1)/(3)\pi \cdot 6^2 \cdot 8}\\\\\displaystyle{V = (1)/(3)\pi \cdot 36 \cdot 8}\\\\\displaystyle{V = \pi \cdot 12 \cdot 8}\\\\\displaystyle{V=96\pi \ \: \text{ft}^3}`

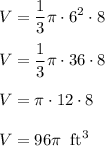
Therefore, the statement B is true.

C- The volume of the cylinder is 288π ft³

Finding the volume of cylinder, the volume's formula is
`\displaystyle{V = \pi r^2 h}`. Substitute known values:

`\displaystyle{V = \pi \cdot 6^2 \cdot 8}\\\\\displaystyle{V = \pi \cdot 36 \cdot 8}\\\\\displaystyle{V=288\pi \ \: \text{ft}^3}`

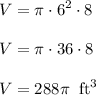
Therefore, the statement C is also true.

D- The area of the base is 36π ft²

Finding the base's area, our base of cylinder is a circle shape. Therefore, the area of circle is
`\displaystyle{A=\pi r^2}`. Thus:

`\displaystyle{A=\pi \cdot 36}\\\\\displaystyle{A=36\pi \ \: \text{ft}^2}`

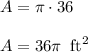
Hence, the statement D is also true.

Therefore, every statements are true. Hence, All of the answers listed are correct answers.