Question

I’m not sure how to solve this

Answer 1

Answers: a = 10, b = 4

=============================================

Step-by-step explanation:

Let's solve for y.

x/a - y/b = 1

x/a = 1 + y/b

y/b = x/a - 1

y = b(x/a - 1)

y = (b/a)x - b

The gradient, aka slope, of this line is b/a. Use the template y = mx+c where m is the slope and c is the y intercept.

We're told the slope is 2/5, so,

b/a = 2/5

5b = 2a

a = 5b/2

a = 2.5b

We'll use this later.

-----------------

Let's return to x/a - y/b = 1.

Plug in y = 0, and solve for x, to get x = a. Therefore, the x intercept is (a,0)

Plug in x = 0, and solve for y, to get y = b. Therefore, the y intercept is (0,b)

I skipped the steps for these two parts, but let me know if you need me to show them.

It turns out that x/a - y/b = 1 is known as intercept form because we can quickly read off the x and y intercepts of (a,0) and (0,b) respectively.

The values of a and b cannot be zero.

Recall that a = 2.5b was found earlier.

So the x intercept updates to (a,0) = (2.5b, 0)

-----------------

We know that segment PQ goes through (2.5b,0) and (0,b) which are the x and y intercepts.

We'll use the distance formula, and the fact segment PQ is 2*sqrt(29) units long to solve for b.

`(x_1,y_1) = (2.5b,0) \text{ and } (x_2,y_2) = (0,b)\\\\d = √( (x_1-x_2)^2+(y_1-y_2)^2 )\\\\d = √( (2.5b-0)^2+(0-b)^2 )\\\\d = √( (2.5b)^2+(-b)^2 )\\\\d = √( 6.25b^2+b^2 )\\\\d = √( 7.25b^2 )\\\\`

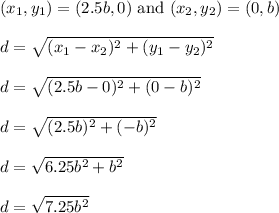
Let's plug in the given distance to be able to solve for b.

`2√(29) = √( 7.25b^2 )\\\\(2√(29))^2 = (√( 7.25b^2 ))^2\\\\116 = 7.25b^2\\\\b^2 = 116/(7.25)\\\\b^2 = 16\\\\b = √(16)\\\\b = 4\\\\`

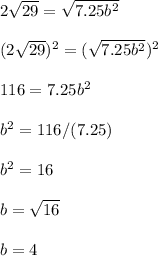
We don't worry about the minus part because we're told a and b are positive.

Use that value of b to find 'a'.

a = 2.5b

a = 2.5*4

a = 10

-------------------------

We found that: a = 10, b = 4

This will make x/a - y/b = 1 update to x/10 - y/4 = 1 and it has (10,0) and (0,4) as the x and y intercepts respectively.

The distance between (10,0) and (0,4) is...

`(x_1,y_1) = (10,0) \text{ and } (x_2, y_2) = (0,4)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((10-0)^2 + (0-4)^2)\\\\d = √((10)^2 + (-4)^2)\\\\d = √(100 + 16)\\\\d = √(116)\\\\d = √(4*29)\\\\d = √(4)*√(29)\\\\d = 2√(29)\\\\d \approx 10.77033\\\\`

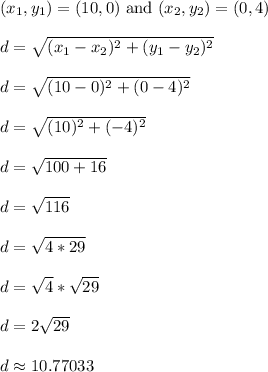
which helps confirm the answer.

Also notice that solving x/10 - y/4 = 1 for y leads to y = (2/5)x - 4, which confirms the slope is 2/5.

The answer has been fully confirmed.