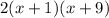Question

3.4 MIXED FACTORING

1. Utilize all of the strategies for factoring in order to factor the following polynomials.
Reminder: Combine like-terms prior to factoring.

(2x^2 + 23x) - (3x - 18)

Answer 1

2 (x + 1)(x + 9)

Explanation:

The given expression is

`\left(2x^2\:+\:23x\right)\:-\:\left(3x\:-\:18\right)`

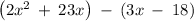
and we are asked to factor it

Step 1
Remove parentheses

`\left(2x^2\:+\:23x\right) = 2x^2 + 23x\\\\-\:\left(3x\:-\:18\right) = - (3x) - (-18) = -3x + 18\\\\`

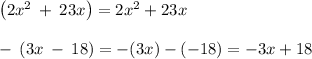
Step 2
Add the individual terms to correspond to the original expression:

`\left(2x^2\:+\:23x\right)\:-\:\left(3x\:-\:18\right) \\\\= 2x^2 + 23x -3x + 18\\\\= 2x^2 + 20x + 18`

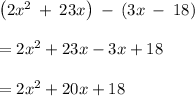
Step 3
Factor out common term 2

`2x^2+20x+18 \\\\= 2\left(x^2+10x+9\right)`

Step 4
Factor
`x^2+10x+9`

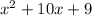
To do this find two numbers such that their sum = 10 and product = 9
We can easily see that these two numbers are 1 and 9 because 1 + 9 = 10 and 1 x 9 = 9

Therefore, splitting the expression into groups we get

`x^2 + 10x + 9 = x^2 + 1x + 9x + 9\\\\`

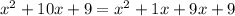
Step 5

Factor:

`x^2 + 1x = x(x+ 1)\\9x + 9 = 9(x + 1)\\\\`

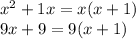
Therefore

`x^2 + 1x + 9x + 9 = x(x + 1) + 9(x + 1)\\\\`

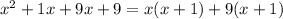
Step 6

Factor common term (x + 1) from the expression

`x(x + 1) + 9(x + 1) = (x + 1)(x + 9)`

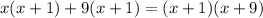
Step 7
Putting it all together
Remember we factored out the 2 in step 3 so we got to put it back into the factored expression giving the final factored expression as

`2 (x + 1)(x + 9)`