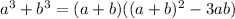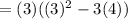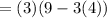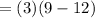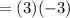Question

If a+b=3 and ab=4 find the value of a3+b3

Answer 1

-9

Explanation:

Recall the following relationships about the sum of cubes and a square binomial:

`a^3+b^3=(a+b)(a^2-ab+b^2)`

`(a+b)^2=a^2+2ab+b^2`

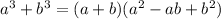
The second factor on the right hand side of equation 1 looks similar to the right hand side of equation 2, but differs slightly.

Carefully choosing to subtract 3ab from both sides of the equation 2, and Combining like terms yields...

`(a+b)^2-3ab=a^2-ab+b^2`

This now matches the second factor on the right hand side of the first equation. So, with substitution, the first equation becomes:

`a^3+b^3=(a+b)(a^2-ab+b^2)`

`a^3+b^3=(a+b)((a+b)^2-3ab)`

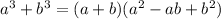
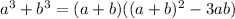
Note that all of the parts on the right hand side of the equation are given in the question:

a+b=3 and ab=4

With some substitution and simplification

`a^3+b^3=(a+b)((a+b)^2-3ab)`

`=(3)((3)^2-3(4))`

`=(3)(9-3(4))`

`=(3)(9-12)`

`=(3)(-3)`

`=-9`