Question

A certain one-dimensional conservative force is given as a function of x by the expression F = -kx^3, where F is in newtons and x is in meters. A possible potential energy function U for this force is

Answer 1

Choice D

Step-by-step explanation:

F(x) = -kx^3

Integrate F(x) with respect to x:

U(x) = - ∫ F(x) dx

= - ∫ (-kx^3) dx

= k/4 * x^4 + C

C is a constant of integration. Find C by specifying the potential energy at a particular value of x. To make it easy, assume that U = 0 at x = 0:

U(0) = k/4 * 0^4 + C = 0

C = 0

Therefore, the potential energy function for the given force F = -kx^3 is:

U(x) = k/4 * x^4

Choice D: U =
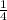`(1)/(4)`kx⁴