Question

A triangle has one angle that is 8 degrees more than twice another of its angles. The two smaller angles are equal in measure. Find the measure of all the angles.​

Answer 1

The measure of both of the smaller angles is 43°.

The measure of the larger angle is 94°.

Explanation:

We can model the larger angle in relation to the smaller angle by representing each of the smaller angles (which are equal in measure) as a variable x and the larger angle as a variable y.

`y = 2x + 8`

This shows that the larger angle is eight degrees more than twice (2 times) the smaller angles' measures.

We can now model the sum of all the triangle's angle measures because we know that a triangle's interior angle measures add to 180°.

`2(\text{small}) + \text{large} = 180`

`2x + y = 180`

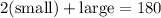
What we have now is a system of equations which we can solve for using substitution. The first equation (
`y = 2x + 8`) is a definition of y in terms of x, so we can substitute that definition into the second equation and solve for x.

`\begin{cases} y = 2x + 8 \\ 2x + y = 180\end{cases}`

`2x + (2x + 8) = 180`

`4x + 8 = 180`

`4x = 172`

`\boxed{x = 43\textdegree}`

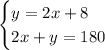
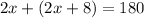
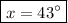
So, the measure of each of the smaller angles is 43°.

Now, we can plug that x-value back into the first equation and solve for y.

`y = 2(43) + 8`

`y = 86 + 8`

`\boxed{y = 94\°}`

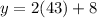
So, the measure of the larger angle is 94°.