Question

How do you find the limit of this sequence?

Please be detailed!!​

Answer 1

0

Explanation:

The limit of a sequence is the value that its terms approach.

We can present the limit of the terms in the sequence as:

`\lim_(n \to \infty)(1)/(n^n)`

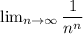
To evaluate this limit, we can plug infinity (the value that n is approaching) into the expression:

`\lim_(n \to \infty)(1)/(n^n)`

`= (1)/(\infty^\infty)`

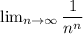
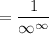
We know that infinity to any positive power is still infinity. So, this expression simplifies to:

`= (1)/(\infty)`

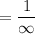
Any real number, no matter how large, is inconsequential (infinitely small) compared to infinity. Therefore, this expression evaluates to 0:

`= 0`

So, the limit of the sequence
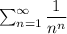`\sum_(n=1)^(\infty) (1)/(n^n)` is 0.

__

Note: You could also deduce the limit of this sequence by plugging in larger and larger numbers:

`\begin{array} cn & \text{seq. term} & \text{decimal} \\\cline{1-3} 2 & 1/4 & 0.25 \\3 & 1/81 & 0.012\\4 & 1/256 & 0.0039 \\5 & 1/3125 & 0.00032 \\... & ... & ... \\\infty & 1/\infty & 0\end{array}`