Question

Could someone help with this question??

Answer 1

(i)
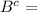`B^c =` {1, 4, 6, 8}

(ii) A - (B - C) = {4, 6, 8}

(iii) A ∩ (B ∪ C) = {2, 3, 5, 7}

Explanation:

We have the following sets

Universal set U = {x ∈ N, x ≤ 8}
This would all the numbers from 1 to 8 inclusive
U = {1, 2, 3, 4, 5, 6, 7, 8}

Set A = {x : 1 < x² < 65}

This would be all the numbers from U such that the square of those numbers lies between 1 and 65

Thus
A = {2, 3, 4, 5, 6, 7 ,8}
We exclude 1 because 1² = 1 is not included in the set definition
Highest is 8 because 8² = 64 < 65 and also 8 is the highest element in the set U

B = (x ∈ N: x is a prime number less than 10}
B = {2, 3, 5, 7 } these being the prime numbers less than 10

C = {x: x³ + 1 = 0, x ∈N}
if x³ + 1 = 0 ==> x³ = -1 and there is only one value of x that satisfies this relationship and that is x = -1 since (-1)³ = -1 and (-1)³ + 1 = 0

Now that we have enumerated the elements of all 4 sets we can solve the questions

(i)
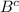`B^c` is the complement of set B = set of all elements not in set B
This would be the set of all numbers from 1 through 8 that are not prime

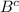`B^c` ={x: x is not a prime number and ≤ 8}

= {1, 4, 6, 8}

(ii) A - (B - C)

B - C is the set difference between B and C

It is the set of all elements in B that are not in C

Since B = {2, 3, 5, 7} and C = {-1} no element of B appears in C so
B - C = B = {2, 3, 5, 7}

A - (B - C) = A - B

{2, 3, 4, 5, 6, 7 ,8} - {2, 3, 5, 7} = {4, 6, 8}

(iii) A ∩ ( B ∪ C)

B ∪ C = {2, 3, 5, 7} ∪ {-1} = {-1, 2, 3, 5, 7}
A ∩ (B ∪ C) = {2, 3, 4, 5, 6, 7 ,8} ∩ {-1, 2, 3, 5, 7}

= {2, 3, 5, 7}

= B

I hope I got it right :)