Question

I need help, I’m struggling with 3 and 4 can someone help me

Answer 1

3 and 4 ==> see work below

`5. \quad\quad f^(-1)(x) = x^(1/7)`

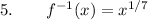
`6. \quad\quad f^(-1)(x) = -\left((5x)/(2)\right)^(1/3)$}\\\text{We can also write this as $-\sqrt[3]{(5x)/(2)}$ }\\`

Explanation:

Definition of inverse functions

If f and g are inverse functions, then f(x) = y if and only if g(y) = x

Or, in other words
If f(g(x)) = (g(f(x)) = x
then f and g are inverse functions

Q3

We have f(x) = x + 4 and g(x) = x - 4

To find f(g(x)), substitute g(x) = x - 4 wherever there is an x term in f(x)

f(g(x)) = g(x) + 4

= x - 4 + 4 = x

g(f(x)) = f(x) - 4

= x + 4 - 4 =x

Hence f(x) and g(x) are inverse functions

Q4

`f(x) = (1)/(4)x^3\\\\g(x) = (4x)^(1/3)`

`\\\begin{aligned}f(g(x)) &= (1)/(4) (g(x))^3\\\\\end{aligned}`

`\begin{aligned}(g(x))^3 &= \left((4x)^(1/3) \right)^3 \\& = (4x)^{(1)/(3) \cdot 3}\\& = 4x\end{aligned}`

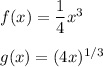
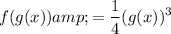
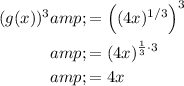
Therefore

`\\\begin{aligned}f(g(x)) &= (1)/(4) (g(x))^3\\&= (1)/(4) \cdot 4x\\&= x\\\end{aligned}`

`\begin{aligned}g\left(f(x)\right) & = \left(4f(x)\right)^(1/3)\\&= \left(4 \cdot (1)/(4)x^3\right)^(1/3)\\& = \left(x^3\right)^(1/3)\\& =x& \end{aligned}`

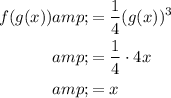
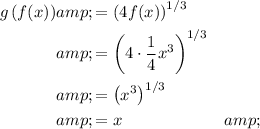
So f(x) and g(x) are inverse functions

Q5

`\text{Given $f(x) = x^7 $ we are asked to find inverse $f^(-1)(x)$}`

`\rm{Let \: y = f(x) = x^7}\\`

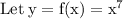
Interchange x and y:

`x = y^7`

Solve for y:

`y = x^(1/7)`

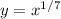
The right hand side is the inverse function of f(x)

`f^(-1)(x) = x^(1/7)`

Q6

`\rm{Given \;f(x) = -(2)/(5)x^3 \:find\:the\:inverse,\;f^(-1)(x)}`

Using the same procedure as for Q5

`y=-(2)/(5)x^3\\\\x=-(2)/(5)y^3\\\\\text{Solve for y}\\`

`y^3=-(5x)/(2)`

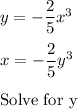
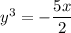
`y=-\left((5x)/(2)\right)^(1/3)\\\\\\\text{Inverse of $f(x)$ is $f^(-1)(x) = -\left((5x)/(2)\right)^(1/3)$}\\\text{We can also write this as $-\sqrt[3]{(5x)/(2)}$ }\\`