Question

The circumference of a wheel is 320.28 centimeters.

Please help.
a) Determine the radius of the wheel.

b) Determine the area of the wheel.

Answer 1

a) The radius of the wheel is 51 cm.

b) The area of the wheel is 8167.14 cm².

Step-by-step Step-by-step explanation:

SOLUTION :

Here we have given that the circumference of a wheel is 320.28 centimeters. We have to find the :

• a) Determine the radius of the wheel.
• b) Determine the area of the wheel.

Finding the radius of circle by substituting all the given values in the formula :

`\quad{\longrightarrow{\sf{C_((Circle)) = 2 \pi r}}}`

• C = circumference
• π = 3.14
• r = radius

`\quad{\longrightarrow{\sf{320.28=2 \pi r}}}`

`\quad{\longrightarrow{\sf{320.28=2 * 3.14 * r}}}`

`\quad{\longrightarrow{\sf{320.28=6.28 * r}}}`

`\quad{\longrightarrow{\sf{r = (320.28)/(6.28)}}}`

`\quad{\longrightarrow{\sf{r = \cancel{(320.28)/(6.28)}}}}`

`\quad{\longrightarrow{\sf{\underline{\underline{\purple{r = 51 \: cm}}}}}}`

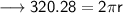
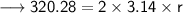
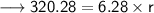
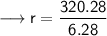
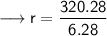
Hence, the radius of circle is 51 cm.

`\begin{gathered} \end{gathered}`

Now, calculating the area of circle by substituting all the given values in the formula

`\quad{\longrightarrow{\sf{A_((Circle)) = \pi {r}^(2)}}}`

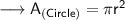
• A = area
• π = 3.14
• r = radius

`\quad{\longrightarrow{\sf{A_((Circle)) = 3.14 {(51)}^(2) }}}`

`\quad{\longrightarrow{\sf{A_((Circle)) = 3.14 {(51 * 51)}}}}`

`\quad{\longrightarrow{\sf{A_((Circle)) = 3.14 {(2601)}}}}`

`\quad{\longrightarrow{\sf{A_((Circle)) = 3.14 * 2601}}}`

`\quad{\longrightarrow{\sf{\underline{\underline{\pink{A_((Circle)) = 8167.14 \: {cm}^(2)}}}}}}`

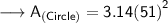
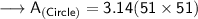
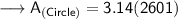
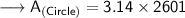
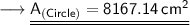
Hence, the area of circle is 8167.14 cm².

————————————————