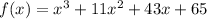Question

Write a polynomial function of least degree with integral coefficients that has the given zeros.

-5, -3-2i

Answer 1

f(x)=x3+11x²+43x+65

Answer 2

`f(x)=x^3+11x^2+43x+65`

Explanation:

If a polynomial function has a complex zero, then the conjugate of that complex zero is also a zero of the polynomial.

So, if (-3 - 2i) is a zero of the polynomial, then its conjugate (-3 + 2i) is also a zero of the polynomial.

Therefore, the three zeros of the polynomial function are:

• -5
• (-3 - 2i)
• (-3 + 2i)

The zero of a polynomial f(x) is the x-value when f(x) = 0.

According to the factor theorem, if f(a) = 0 then (x - a) is a factor of the polynomial f(x).

Therefore, the polynomial function in factored form is:

`\begin{aligned}f(x) &= (x - (-5))(x-(-3-2i))(x-(-3+2i))\\&= (x +5)(x+3+2i)(x+3-2i)\end{aligned}`

Expand the brackets to write the polynomial in standard form.

`\begin{aligned}f(x) &=(x +5)(x+3+2i)(x+3-2i)\\&=(x+5)(x^2+3x-2xi+3x+9-6i+2ix+6i-4i^2)\\&=(x+5)(x^2+6x+9-4i^2)\\&=(x+5)(x^2+6x+9-4(-1))\\&=(x+5)(x^2+6x+9+4)\\&=(x+5)(x^2+6x+13)\\&=x^3+6x^2+13x+5x^2+30x+65\\&=x^3+11x^2+43x+65\end{aligned}`

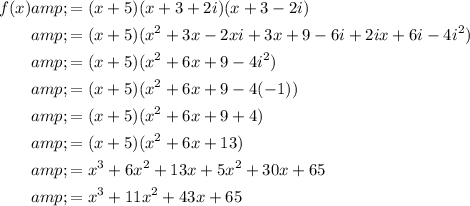
Therefore, the polynomial function of least degree with integral coefficients that has the given zeros -5 and (-3 - 2i) is:

`f(x)=x^3+11x^2+43x+65`