Question

Find an equation in slope-intercept form for the line passing through each pair of points: (-4, 4), (-5, -3)

Answer 1

y = 7x + 32

Explanation:

The general equation of the slope-intercept form is

• y = mx + b, where
• x and y are any point on the line
• m is the slope (change in y / change in x)
• and b is the y-intercept (point at which the line intersects the y-axis)

Given two points which line on the same line, we can find the slope, m, using the slope formula, which is

`m=(y_(2) -y_(1) )/(x_(2)-x_(1) )`,

• where x1 and x2 are one of the points on the line
• and y1 and y2 are the other point.

If we allow (-4, 4) to be our x1 and x2 point and (-5, -3) to be our y1 and y2 point, we can find the slope by plugging the points into the slope formula:

`m=(-3-4)/(-5-(-4))\\ \\m=(-7)/(-5+4)\\ \\m=(-7)/(-1)\\ \\m=7`

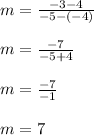
Since we now know the slope, we can b, the y-intercept by plugging in any of the two points for x and y and the slope (7) and solving for b:

Let's try the first point (-4, 4):

4 = 7(-4) + b

4 = -28 + b

32 = b

Thus, the equation of the line passing through the points (-4, 4) and (-5, -3) in slope-intercept form is y = 7x + 32