Question

In △PQR, what is the length of segment QR? Right triangle PQR with PR measuring 56 and angles P and R measure 45 degrees. 28 28radical 2 56radical 3 56radical 2

Answer 1

`\overline{\sf QR}=28√(2)`

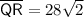
Explanation:

If ΔPQR is a right triangle, where angles P and R both measure 45°, then the triangle is a special 45-45-90 triangle.

The measure of the sides of a 45-45-90 triangle are in the ratio 1 : 1 : √2.

This means that the length of each leg is equal, and the length of the hypotenuse is equal to the length of a leg multiplied by √2.

The legs of ΔPQR are segments PQ and QR.

The hypotenuse of ΔPQR is segment PR.

Therefore, to find the length of the leg QR, divide the length of the hypotenuse PR by √2.

`\begin{aligned}\implies \overline{\sf QR}&=\frac{\overline{\sf PR}}{√(2)}\\\\&= (56)/(√(2)) \\\\&=(56)/(√(2))\cdot (√(2))/(√(2))\\\\&=(56√(2))/(2)\\\\&=28√(2)\end{aligned}`

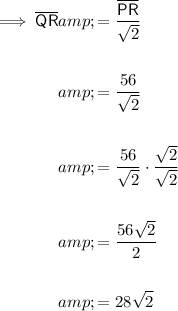
Therefore, the length of segment QR is 28√2.