Question

The question is done below has square roots and exponents. Pretty easy.

Answer 1

Answer: D. -1

Explanation:

Your equation:

`\sqrt[4]{(\sqrt[3]{64}) ^(2) } =((1)/(2) )^(x)` >We are going to work from the inside first then out

The cube root of 64 is 4 because 4*4*4=64

`\sqrt[4]{(4) ^(2) } =((1)/(2) )^(x)` > 4² = 4*4=16

`\sqrt[4]{(16) } =((1)/(2) )^(x)` > the 4th root of 16 is 2 because 2*2*2*2=16

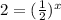`2 =((1)/(2) )^(x)` > if you have the same bases you can set the

exponents equal. They are not the same but we

are going to make them the same.

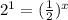`2^(1) =((1)/(2) )^(x)` > 2 is the same as 2^1, i can make the bases the

same if I can make the 2 a reciprocal. That

happens when I take the negative exponent of the

number

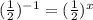`((1)/(2) )^(-1) =((1)/(2) )^(x)` >Now that my bases are the same, I can make the

exponents =

-1 = x