Question

Help pls! Assuming non-ideal behavior, a 2. 0 mol sample of CO₂ in a 7. 30 L container at 200. 0 K has a pressure of 4. 50 atm. If a = 3. 59 L²･atm/mol² and b = 0. 0427 L/mol for CO₂, according to the van der Waals equation what is the difference in pressure (in atm) between ideal and nonideal conditions for CO₂?

Answer 1

The difference in pressure between ideal and non-ideal conditions for CO₂ is approximately 0.22 atm.

The van der Waals equation for a real gas is given by:

`\[ \left(P + (a)/(V^2)\right)(V - b) = RT \]`

For the ideal gas equation, PV = nRT, where n is the number of moles.

First, rearrange the van der Waals equation to solve for P:

`\[ P = (RT)/(V - b) - (a)/(V^2) \]`

Now, calculate the pressure
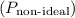`(\( P_{\text{non-ideal}} \))` using the van der Waals equation:

`\[ P_{\text{non-ideal}} = (RT)/(V - b) - (a)/(V^2) \]`

`\[ P_{\text{non-ideal}} = \frac{(2.0 \, \text{mol})(0.0821 \, \text{L} \, \text{atm} \, \text{mol}^(-1) \, \text{K}^(-1))(200.0 \, \text{K})}{7.30 \, \text{L} - 0.0427 \, \text{L}} - \frac{3.59 \, \text{L}^2 \, \text{atm} \, \text{mol}^(-2)}{(7.30 \, \text{L})^2} \]`

`\[ P_{\text{non-ideal}} \approx 4.77 \, \text{atm} \]`

Now, calculate the pressure under ideal conditions
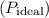`(\( P_{\text{ideal}} \))` using the ideal gas equation:

`\[ P_{\text{ideal}} = (nRT)/(V) \]`

`\[ P_{\text{ideal}} = \frac{(2.0 \, \text{mol})(0.0821 \, \text{L} \, \text{atm} \, \text{mol}^(-1) \, \text{K}^(-1))(200.0 \, \text{K})}{7.30 \, \text{L}} \]`

`\[ P_{\text{ideal}} \approx 4.99 \, \text{atm} \]`

Finally, find the difference in pressure
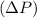`(\( \Delta P \))` between ideal and non-ideal conditions:

`\[ \Delta P = P_{\text{ideal}} - P_{\text{non-ideal}} \]`

`\[ \Delta P \approx 4.99 \, \text{atm} - 4.77 \, \text{atm} \]`

`\[ \Delta P \approx 0.22 \, \text{atm} \]`

So, the difference in pressure between ideal and non-ideal conditions for CO₂ is approximately 0.22 atm.