The force between these charges, according to Coulomb's law would be -54 N.
We can solve this problem applying "Coulomb's Law" which states-
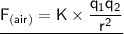

Where-
- q₁ and q₂ are the two cahrges.
- r is the distance between the charges.
 is the permittivity of free space.
is the permittivity of free space.- K is the Coulomb's Constant.
- k = 9×10⁹ Nm²/C²
According to the given parameters -
- Magnitude of q₁= 3 μC
- Magnitude of q₂= -5 μC
- Distance,r = 5cm
Now that required values are given, so we can plug the values into the formula and solve for Force -

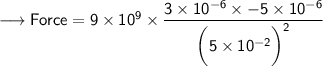
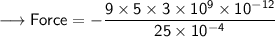
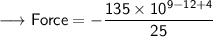
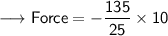
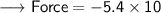
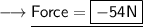
- Henceforth, The force between these charges, according to Coulomb's law would be -54 N.