Question

for the past 15 years, an employee of a large corporation has been investing in an employee sponsored educational savings plan. the employee has invested $8,000 dollars per year. treat the investment as a continuous stream with interest paid at a rate of 4.5% compounded continuously. (a) what is the future value of the investment? (round your answer to the nearest cent.) $ (b) how much money would have had to be invested 15 years ago and compounded at 4.5% compounded continuously to grow to the amount found in part (a)? (round your answer to the nearest cent.) $

Answer 1

The future value of a continuously compounded investment is calculated using an integration of the annual investment over the time period at the given interest rate. The lump sum needed to reach that future value is found by discounting the future value by the same continuous interest rate over the investment period.

Step-by-step explanation:

To calculate the future value of the investment with continuous compounding, we can use the formula for the future value of a continuously compounded investment:

FV =
`P * e^((r*t))`

Where FV is the future value, P is the principal amount, e is the base of the natural logarithm (approximately equal to 2.71828), r is the annual interest rate (in decimal form), and t is the time in years.

However, since the employee invests $8,000 per year, we need to integrate this investing stream over 15 years. The modified formula in this case is:

FV = ∫ P *
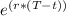`e^((r*(T-t)))`) dt from 0 to T

After computing the integral, we can find the future value and for part (b), we would then find the lump sum P that would amount to that future value using the formula:

P = FV *
`e^((-r*t))`

These calculations will give us the detailed answers required.