Question

Help would be much appreciated.

Answer 1

A) Rotate ΔABC 90° clockwise about the origin.

Explanation:

From inspection of the given diagram, the coordinates of the vertices of triangle ABC are:

• A = (-1, 1)
• B = (-1, 5)
• C = (-4, 2)

The coordinates of the vertices of triangle XYZ are:

• X = (1, 1)
• Y = (5, 1)
• Z = (2, 4)

The mapping rule for a rotation of 90° clockwise about the origin is:

`\boxed{(x, y) \rightarrow (y, -x)}`

Therefore:

• A = (-1, 1) → X = (1, 1)
• B = (-1, 5) → Y = (5, 1)
• C = (-4, 2) → Z = (2, 4)

The mapping rule for a rotation of 90° clockwise about a point P is:

`\boxed{\left([y - y_P + x_P], [x_P - x + y_P]\right)}`

So the mapping rule if the point of rotation is A (-1, 1) is:

`\boxed{(y - 2 , -x)}`

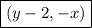
Therefore:

• A = (-1, 1) → X = (-1, 1)
• B = (-1, 5) → Y = (3, 1)
• C = (-4, 2) → Z = (0, 4)

The mapping rule for a reflection across the y -axis is:

`\boxed{(x, y) \rightarrow (-x, y)}`

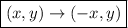
Therefore:

• A = (-1, 1) → X = (1, 1)
• B = (-1, 5) → Y = (1, 5)
• C = (-4, 2) → Z = (4, 2)

The mapping rule for a reflection across the line y = x is:

`\boxed{ (x, y) \rightarrow (y, x)}`

Therefore:

• A = (-1, 1) → X = (1, -1)
• B = (-1, 5) → Y = (5, -1)
• C = (-4, 2) → Z = (2, -4)

Solution

Comparing the different transformations, we can see that the rigid motion that could be used to map triangle ABC onto triangle XYZ is:

• Rotate ΔABC 90° clockwise about the origin.