Question

A right triangle has two legs measuring 9 and 40 respectively, what is the length of the hypotenuse?

Answer 1

The length of the hypotenuse is 41.

Explanation:

The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

In this case, the lengths of the legs are 9 and 40. Using the Pythagorean theorem, we can find the length of the hypotenuse:

`\sf:\implies h^2 = 9^2 + 40^2`

`\sf:\implies h^2 = 81 + 1600`

`\sf:\implies h^2 = 1681`

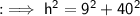
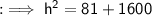
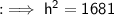
Taking the square root of both sides, we get:

`\sf:\implies h = √(1681)`

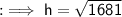
Simplifying the square root, we get:

`\sf:\implies \boxed{\bold{\:\:h = 41\:\:}}\:\:\:\green{\checkmark}`

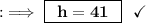
Therefore, the length of the hypotenuse is 41.

Greetings! ZenZebra at your service, hope it helps! <33