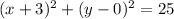Answer:
1.

2.
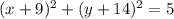
3.

4.
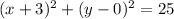
For Questions 1-2:
Step 1: Formula
The standard form of a circle is
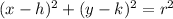 .
.
The h represents the x value of the coordinates of the circle's center and the k is the y value of the coordinates. The r is the radius.
So in the first problem h is going to be 3 and k is going to be -15. (In this problem the signs are flipped, so if you have a positive number it will be negative in the formula)
After inserting the values in the formula you have your answer of
 . Now let us find the radius
. Now let us find the radius
Step 2: Find the radius
To find the radius of the first two problems what you can do is you can use the distance formula.
To use the distance formula you find have to identify the (x1, y1) and the (x2, y2)
In the first problem, the (x1, y1) would be the center of the circle. The reason for this is that on a graph you have to read it left to right (kinda like English) so to find the values you have to imagine what values would come first, in this case, the center point would come first.
So let us input the values in the formula. The formula is
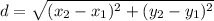 . This is the distance formula, this formula will be used in this problem.
. This is the distance formula, this formula will be used in this problem.
Okay so the x1 is 3 and the y1 is -15. The x2 is 0 and the y2 is -13. So lets us input these values.

3.605 is our radius.
Now let us write our finished equation.
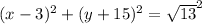 or
or
 .
.
Doing these steps for the next problem gives us our second answer of
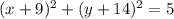
For Questions 3-4:
Step 1: Midpoint Formula
To solve this problem you need to use the midpoint formula. The midpoint formula is
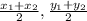 . In the first problem, the x1 would be -10, the y1 would be -13. The x2, on the other hand, is 4 and the y2 is -9. Now find the center of the circle.
. In the first problem, the x1 would be -10, the y1 would be -13. The x2, on the other hand, is 4 and the y2 is -9. Now find the center of the circle.
Step 2: Find the center
To find the center of the circle we need to insert the values of x and the values of y into the midpoint formula. We can do this because they gave us the diameter and the diameter goes through the middle of the circle. So we can do this.

So (-3, -11) is the center of the circle.
Step 3: Find the radius
Now that we have the center of the circle we can use the distance formula to find the radius. We already have two of the ends of the radius so we can simply use the distance formula with the center and the ends.

Step 4: Write your final equation
Know we can insert all the values we have into the standard form of a circle equation.
 or
or
 . This is our answer.
. This is our answer.
Doing these steps for the next problem gives us our answer of